COCI '20 Contest 1 #3 3D Histogram
View as PDFMr. Malnar (over the phone): Listen, I had to put up some posters around Zagreb in the middle of the night. I stumbled upon a fence that was made out of some planks of varying heights, and I was thinking about how to calculate the largest area of a poster that I can fit on the fence. Wouldn't that make a nice COCI problem?
Associate: You were doing what?! Anyway, the problem is no good. It's a standard trick with a monotone queue, we even teach that to elementary school students on our camps.
Mr. Malnar: What if you twist it a bit, ask for the answer for every prefix or something like that, that should be hard enough.
Associate: That exact problem was featured last year in our CERC qualification contest. A tough one, it boils down to the Harbingers trick, but now everyone has seen it.
Mr. Malnar: Are you sure there is nothing we can do?
Associate: I think we have exhausted all problems with histograms. COCI 2010/2011 (Tabovi), COCI 2015/2016 (Poplava), COCI 2017/2018 (Krov), IOI selection test 2018 (Histogram)… You get the point.
Mr. Malnar: What if the histogram is three-dimensional?
Associate: Umm…
You are given a 3D histogram, that consists of blocks that are placed next to each other. The
-th
block is
meter wide,
meters tall and
meters long. In other words, from the front it looks like a
histogram with bars of heights
, and from the top it looks like a histogram with bars of heights
.
Determine the block with maximum volume that can be placed inside the given 3D histogram. The sides of that block need to be parallel with the sides of the blocks that make up the 3D histogram.
Input
The first line contains the integer from the task description.
The
-th of the following
lines contains integers
and
from the task description.
Output
Print the volume in cubic meters.
Scoring
| Subtask | Score | Constraints |
|---|---|---|
Sample Input 1
5
5 3
4 4
2 1
3 2
1 5Sample Output 1
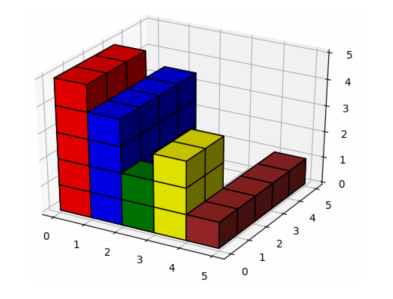
24Explanation for Sample Output 1
The figure below shows the 3D histogram from the first example. The largest block is obtained using
parts of the first two blocks, and it is meters wide,
meters tall and
meters long. The volume of the
block is
cubic meters.
Sample Input 2
6
3 1
2 1
2 2
2 3
1 1
2 2Sample Output 2
8Sample Input 3
5
15 19
5 6
1 13
3 7
1 2Sample Output 3
285
Comments