Subtask 1

This question can be modelled as a graph, with classrooms as nodes and hallways (or tunnels) as edges. Since there are ~N-1~ hallways and you can travel between any two classrooms via those hallways, the graph is a tree. Keep track of the number of students in each classroom with an array. For every update event, increment or decrement the counts accordingly. For every query event, temporarily add the tunnel to the graph and run a BFS from classroom ~1~ to determine the shortest distance from it to every classroom in the school. Then, for every classroom, multiply its distance from classroom ~1~ by the number of students currently in it, and add up all of these values to determine the total cost of delivering candygrams. Then, remove the tunnel from the graph so as to not affect future query events.

Time Complexity: ~\mathcal{O}(NQ)~

Subtask 2

Let's analyze how adding an tunnel from classroom ~A~ to classroom ~B~ affects the distances more closely. Denote ~D_x~ as the distance from ~x~ to classroom ~1~. Without loss of generality, assume ~D_A \le D_B~. Then it is never optimal to go from ~B~ to ~A~, since we could just go to ~A~ directly in less than or equal the same amount of distance. Now, let us consider which classrooms have become closer to classroom ~1~ by taking advantage of going from ~A~ to ~B~. Any classroom in the subtree of ~B~ will have their distance reduced by ~D_B - D_A~. However, it may also be optimal for some classrooms to travel to ~A~, then use the tunnel to go to ~B~, travel up the tree, and go down a different subtree.

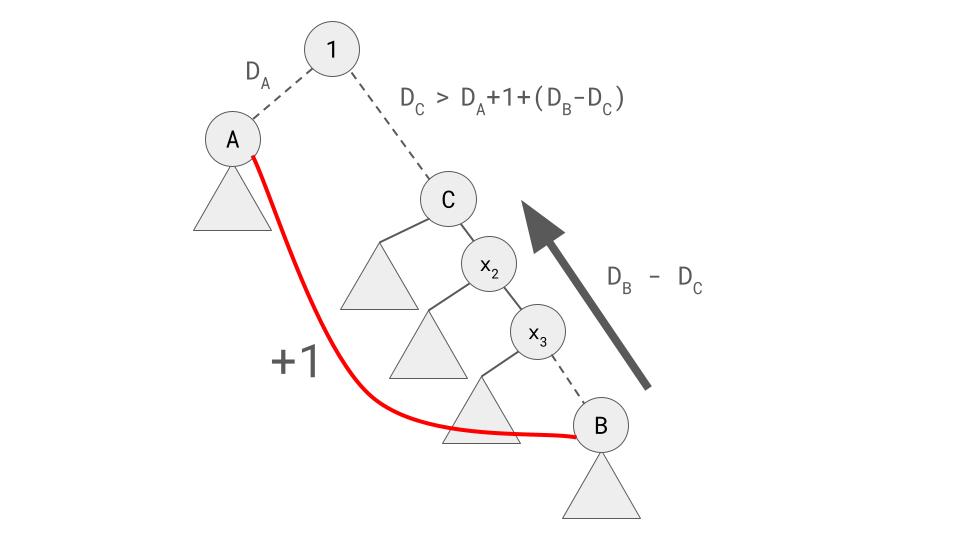
Let the highest ancestor of ~B~ whose distance is reduced this way be ~C~. In other words, ~C~ is the highest node which satisfies ~D_C > D_A + 1 + (D_B - D_C)~. Consider the path of nodes from node ~C~ to node ~B~, say, ~x_1, x_2, \dots, x_m~. All the students in ~x_1~'s subtree will have their distance reduce by ~1~ or ~2~ depending on the parity of ~D_B - D_A~, all the students in ~x_2~'s subtree will have their distance reduce by an additional ~2~, all the students in ~x_3~'s will have their distance reduce by an additional ~2~, and so on until all the students in ~x_m~'s subtree will have their distance reduce by an additional ~2~.

To dynamically maintain the number of students in each node's subtree, and to perform sum queries along the path from ~C~ to ~B~, we can use HLD. Finding node ~C~ may also require an additional query.

Time Complexity: ~\mathcal{O}(N + Q \log^2 N)~