Bob the archaeologist is searching for a treasure in a mysterious labyrinth! The labyrinth consists of $N$ rooms numbered $1$ to $N$, which are connected by exactly $N-1$ bidirectional corridors of varying length. The $i^{\text{th}}$ corridor connects rooms $u_i$ and $v_i$ and takes $t_i$ seconds to traverse. It is guaranteed that every room is reachable from any other room.

Hidden around these rooms are $M$ mysterious locked boxes, numbered $1$ to $M$. The $i^{\text{th}}$ box can be found in room $r_i$ and contains exactly $k_i$ keys. The $j^{\text{th}}$ key in the $i^{\text{th}}$ box can open box $o_{i,j}$. The treasure is located in box $T$.

Bob starts in room $1$ with $S$ keys, which can open the boxes $s_1,s_2,\dots ,s_S$. Since Bob is infinitely intelligent and efficient, he will always take the optimal route to obtain the treasure. Is it possible for Bob to open the box with the treasure, and if so, what is the minimum number of seconds it will take him to do so?

Constraints

$2\le N\le {10}^5$

$1\le u_i,v_i\le N$

$1\le t_i\le {10}^4$

Every room is reachable from every other room.

$1\le M\le {10}^5$

$1\le T\le M$

$1\le r_i\le N$

$0\le k_i\le 3$

$1\le o_{i,j}\le M$

$1\le S\le M$

$1\le s_i\le M$

Subtask 1 [20%]

$2\le N\le 2000$

Subtask 2 [80%]

No additional constraints.

Input Specification

The first line contains the integer $N$, the number of rooms.

The $i^{\text{th}}$ of the following $N-1$ lines contains the integers $u_i$, $v_i$, and $t_i$, representing the two ends of each corridor and the time it takes to traverse it.

The next line contains two integers, $M$ and $T$, the number of mysterious boxes and the box the treasure is located in.

The next line contains $M$ integers, $r_1,r_2,\dots ,r_M$, the rooms each box is located in.

The $i^{\text{th}}$ of the following $M$ lines contain the integer $k_i$, followed by $k_i$ integers $o_{i,1},o_{i,2},\dots ,o_{i,k_i}$. These denote the number of keys contained in each box and the box that each key opens.

The next line contains the integer $S$, the number of keys that Bob starts with.

The last line contains $S$ integers, $s_1,s_2,\dots ,s_S$, the boxes that Bob can open with each of the starting keys.

Output Specification

If it is possible to open the box with the treasure, output the minimum number of seconds it will take Bob to do so. Otherwise, output $-1$.

Sample Input

10
6 1 4
4 8 10
4 6 3
5 8 7
2 7 8
8 9 2
6 10 9
1 3 4
9 2 4
10 3
5 3 5 6 2 9 10 3 4 5
3 2 8 10
1 10
0
2 5 7
1 1
2 7 8
3 3 3 10
1 3
2 2 6
1 3
2
6 6

Sample Output

70

Explanation for Sample Output

The rooms and boxes are arranged like this:

'$x[o_{x,1},o_{x,2},\dots ,o_{x,k_x}]$' represents box $x$ with keys to boxes $o_{x,1},o_{x,2},\dots ,o_{x,k_x}$. '$x[!]$' represents box $x$ with the treasure.

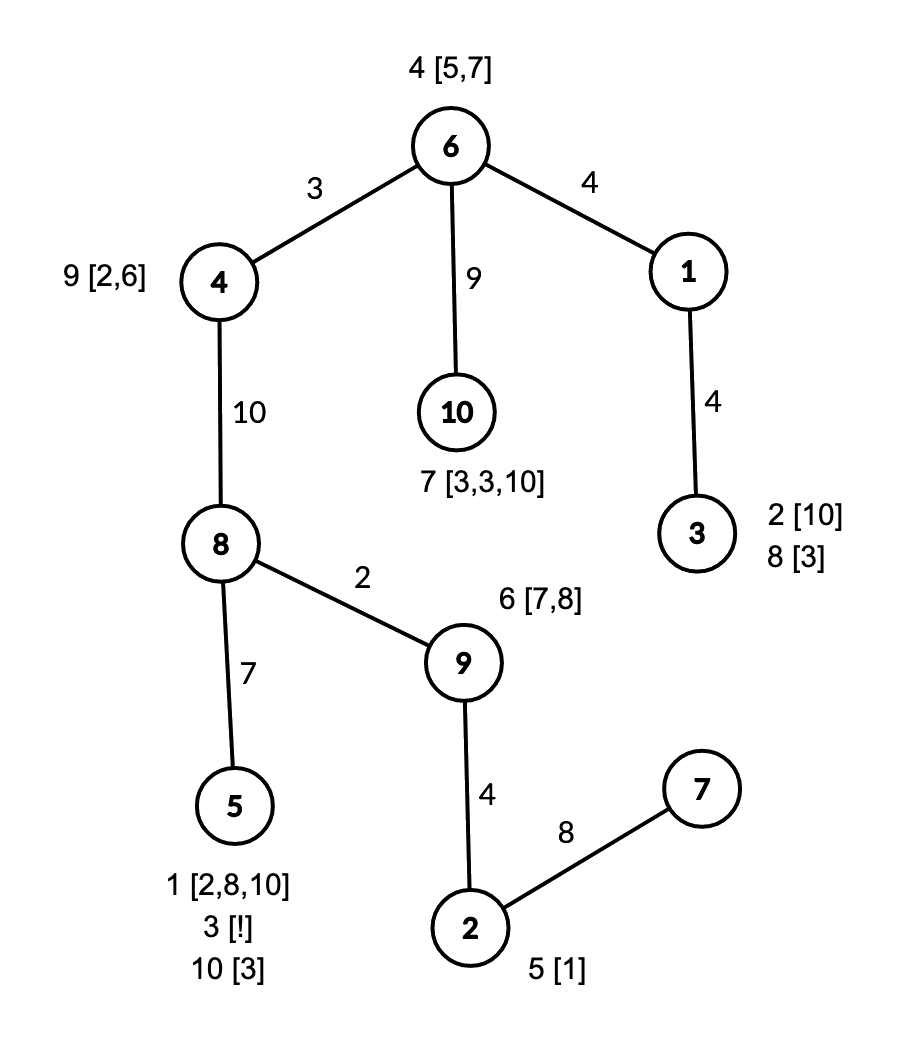
Bob can go to from room $1$ to room $9$ to open box $6$, obtaining keys to boxes $7$ and $8$ after $19$ seconds.

He can then go from room $9$ to room $3$ to open box $8$, obtaining a key to box $3$ after an additional $23$ seconds.

He can then go from room $3$ to room $5$ to open box $3$, obtaining the treasure after an additional $28$ seconds.

The total time taken is $19+23+28=70$ seconds. It can be proven that this is the minimum time.