On a warm spring day, Tony ventures into one of Unionville's many parks. The park can be modelled as a ~2 \times N~ grid, with the cell in the ~r^\text{th}~ row and the ~c^\text{th}~ column denoted as ~(r, c)~.

Tony is currently standing at ~(1, 1)~, the top-left cell. In one minute, he can move to an adjacent cell that is above, below, to the left, or to the right of him. Tony wants to end up at ~(1, N)~, the top-right cell, but he quickly realizes that the shortest path to this cell is too short for him to enjoy the amazing scenery that Unionville has to offer!

Fortunately, Tony has an unlimited supply of trees which he can place on different cells to make his journey longer. Tony cannot move to a cell that has a tree, and he must make sure that a path from ~(1, 1)~ to ~(1, N)~ still exists. Help Tony find the maximum possible length of the shortest path from ~(1, 1)~ to ~(1, N)~ after placing the trees optimally!

Note: Tony cannot place a tree on the starting cell ~(1, 1)~ or ending cell ~(1, N)~.

Constraints

~2 \le N \le 10^9~

Input Specification

The first line contains one integer, ~N~.

Output Specification

Output the maximum possible length of the shortest path from ~(1, 1)~ to ~(1, N)~.

Sample Input 1

4

Sample Output 1

5

Explanation for Sample Input 1

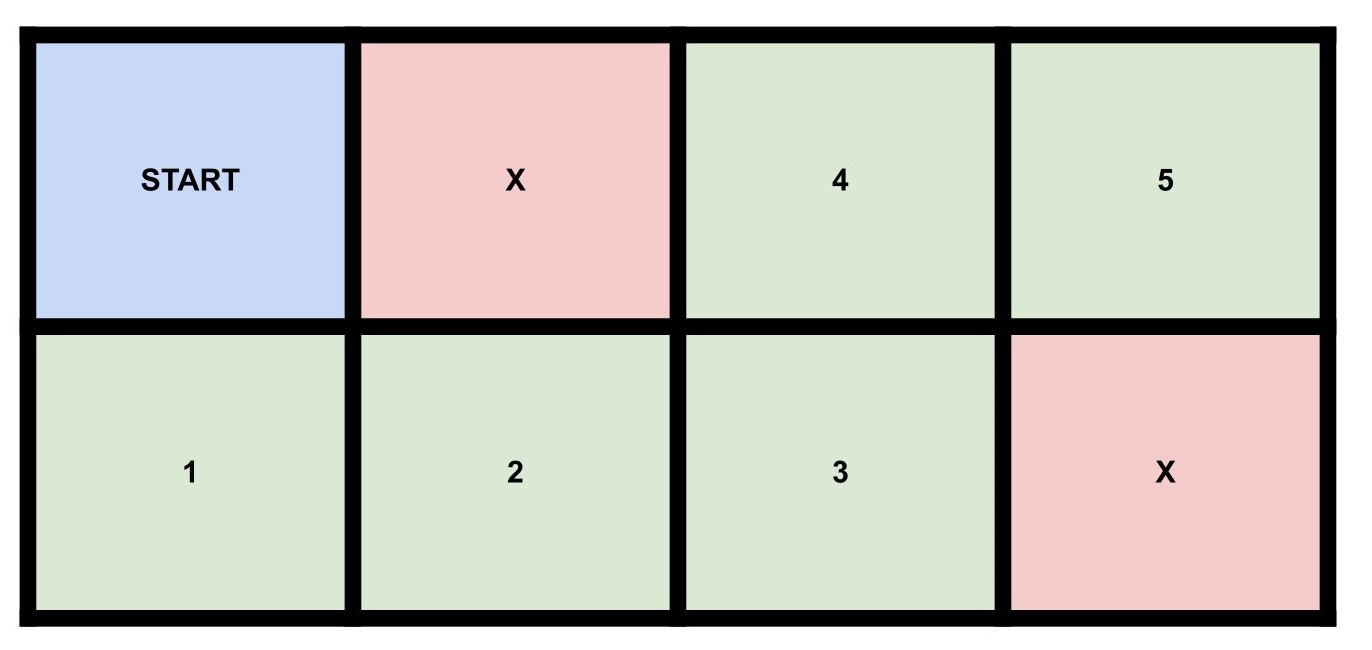
Note that other possible configurations exist.

Sample Input 2

12

Sample Output 2

17