National Olympiad in Informatics, China, 1999
July 17th is Mr. W's Birthday, and ACM-THU would like to
create for him a birthday cake with volume 
~N\pi~, comprised of 
~M~
cylindrical layers.
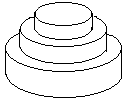
Counting upwards from the bottom layer, the 
~i~-th 
~(1 \le i \le M)~
layer of cake is a cylinder with a radius of 
~R_i~ and a height of
~H_i~. When 
~i < M~, we require for 
~R_i > R_{i+1}~ and 
~H_i > H_{i+1}~.
To reduce the money spent on icing the cake, we would like to minimize
~Q~, the outer surface area of the cake (not including the bottom
surface of the bottommost layer).
Let 
~Q = S\pi~. Please write a program that, given 
~N~ and ~M~, finds a
strategy to construct the cake (with appropriate ~R_i~ and ~H_i~
values) that minimizes the value of 
~S~.
Other than ~Q~, all values described above will be positive integers.
Input Specification
The input will consist of two lines. The first line is the integer ~N~
~(N \le 10\,000)~, indicating that the volume of the cake is ~N\pi~. The
second line of input is the integer ~M~ 
~(M \le 20)~, representing the
number of levels in the cake.
Output Specification
The output should consist of one line - a positive integer ~S~ (if no
answer, 
~S = 0~).
Sample Input
100
2
Sample Output
68
Formulas for cylinders:
Volume: 
~V = \pi R^2H~
Side surface area: 
~A' = 2\pi RH~
Bottom surface area: 
~A = \pi R^2~
Problem translated to English by Alex.
Comments