National Olympiad in Informatics, China, 1998

The tailor has a very precious scarf. Unfortunately, parts of the scarf have been ruined by moth bites. Obviously, he doesn't want to just throw it away, so he decides to cut the scarf into two little scarves to give to his two daughters. Of course, the larger the total area between the two scarves, the better.

His scarf is currently an equilateral triangle that has been evenly split into $N$ (horizontal) sections. Furthermore, it has been evenly divided into $N^2$ cells. Each cell is an equilateral triangle with an area of 1. The figure below depicts a scarf for $N=5$. The shaded area represents the cells which have been bitten by moths. From top to bottom, the triangle is divided into $N$ rows, where the first row has 1 cell, and the second row has 3 cells in which two have the shape △ and 1 has the shape ▽ (these two types of triangles we shall consider congruent). The third line has 5 cells, in which 3 have the shape △ and 2 have the shape ▽, and so on. Using coordinates $(x,y)$ to denote the position of cells, the first row's cell has the coordinate $(1,1)$; the cells in the second row have coordinates $(2,1)$, $(2,2)$, $(2,3)$ respectively; …

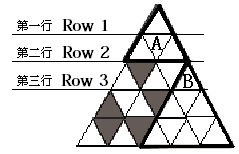
The rules for cutting the scarf is as follows:

1. The shape of the two smaller triangles must be exactly the same as the larger one (equilateral).
2. Neither of the smaller triangles should contain moth bitten cells.
3. Cuts may only be made on the borders of cells.
4. The total area of the two small triangles must be maximized.

In the diagram above, the best way to cut is along the bolded lines, for a total area of $4+9=13$. You are to write a program that solves this problem for the tailor.

Input Specification

The first line of input contains the integer $N$ $(1\le N\le 100)$, indicating that the scarf consists of $N^2$ total cells. The second line contains the integer $M$ $(0\le M\le N^2-2)$, the number of cells that have been bitten by moths. There will be $M$ lines to follow with two integers $x$ and $y$ on each line, giving the coordinates of the moth-bitten cells. Adjacent numbers in the input may be separated by one or more spaces.

Output Specification

You should output one integer - the maximum possible value for the total area between the two smaller triangles if the tailor cuts optimally.

Sample Input

5
5
3 2
4 1
4 4
5 4
5 2

Sample Output

13

Problem translated to English by Alex.