National Olympiad in Informatics, China, 2014

This summer, NOI is celebrating her 30th birthday in city SZ. The OIers from $n$ cities across the nation will arrive in city SZ to participate in the celebration.

The $n$ cities in the nation form a tree rooted at city SZ. Each city is connected to its parent by a road. For the sake of simplicity, we have numbered the $n$ cities with unique integers from $1$ to $n$. City SZ is numbered $1$. Outside of city SZ itself, any city $v$ will have a parent denoted by $f_v$, connected by a road of length $s_v$.

Traveling from city $v$ to city SZ can be done in the following way: Select an ancestor $a$ of city $v$, pay the ticket cost, and take the public transit to city $a$. Then, pick ancestor $b$ of city $a$, pay the ticket, and travel there. Repeat this process until city SZ is reached.

For any city $v$, we place a limit $l_v$ on the distance of the public transit. For an ancestor $a$ of $v$, if and only if the total distance of all the roads between $a$ and $v$ does not exceed $l_v$, then it's possible to go straight to city $a$ from $v$ by buying one ticket. For each city $v$, we can also provide two nonnegative integers $p_v$ and $q_v$ as the ticket price parameters. If we let the total distance of all roads from $v$ to $a$ equal $d$, then the ticket cost to travel from $v$ to $a$ is $d\times p_v+q_v$.

OIers from all the cities wish to reach city SZ by themselves with the smallest total cost. Your task is to tell the OIers from each city the minimum possible cost they will need to pay to reach city SZ.

Input Specification

The first line of input will contain two nonnegative integers $n$ and $t$, respectively representing the number of cities and the type of the test case (explained below).
Lines 2 to $n$ of the input will each describe a city outside of city SZ. Line $v$ will contain five nonnegative integers $f_v$, $s_v$, $p_v$, $q_v$, and $l_v$, respectively representing the parent of city $v$, the length of the road to its parent, the ticket price parameters, and the distance limit.
Note: the input will not contain city SZ which is numbered $1$. Line 2 to line $n$ will respectively represent the cities numbered from $2$ to $n$.

Output Specification

Output $n-1$ lines, each line containing a single integer. Line $v$ should indicate the minimum total ticket cost if an OIer wanted to travel from city $v+1$ to city SZ.
Note again: the output should not include city SZ which is numbered $1$.

Sample Input

7 3
1 2 20 0 3
1 5 10 100 5
2 4 10 10 10
2 9 1 100 10
3 5 20 100 10
4 4 20 0 10

Sample Output

40
150
70
149
300
150

Explanation

Refer to the diagram below:

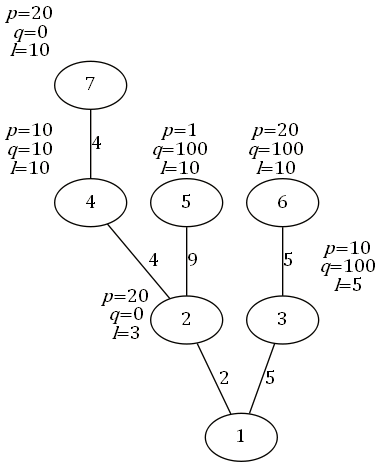
The paths to travel to SZ from every city is outlined as follows (where arrows represent a single, direct trip):
City 2: Only $2\to 1$ is possible, for a cost of $2\times 20+0=40$.
City 3: Only $3\to 1$ is possible, for a cost of $5\times 10+100=150$.
City 4: Since $4+2=6\le l_4=10$, one route is $4\to 1$. If this is selected, then the cost will be $(4+2)\times 10+10=70$. If instead the route $4\to 2\to 1$ is chosen, then the cost will be $(4\times 10+10)+(2\times 20+0)=90$. Thus, the best route is $4\to 1$.
City 5: Only $5\to 2\to 1$ is possible, for a cost of $(9\times 1+100)+(2\times 20+0)=149$. $5\to 1$ is not valid – since $l_5=10$, and city 5 to city 1's total distance is $9+2=11>l_5$, 5 cannot directly reach 1.
City 6: If $6\to 1$ is selected, the cost will be $(5+5)\times 20+100=300$. If $6\to 3\to 1$ is selected, the cost will be $(5\times 20+100)+(5\times 10+100)=350$. Thus, the best route is $6\to 1$.
City 7: Choose $7\to 4\to 1$ for a cost of $(4\times 20+0)+((4+2)\times 10+10)=150$. All other methods are suboptimal to this.

Constraints

All of the test cases satisfy $0\le p_v\le {10}^6$, $0\le q_v\le {10}^{12}$, $1\le f_v<v$, and $0<s_v\le l_v\le 2\times {10}^{11}$. Also, the total distance between any city and city SZ will not exceed $2\times {10}^{11}$.

The input value $t$ represents the type of test case, $0\le t<4$:
When $t=0$ or $2$, each of the input cities $v$ will have $f_v=v-1$. That is, the cities will form a chain with SZ at one end.
When $t=0$ or $1$, each of the input cities $v$ will have $l_v=2\times {10}^{11}$. That is, there will be no distance limit for traveling between cities – every city will be able to reach every one of its ancestors.
When $t=3$, there will be no special characteristics for the test case.
The sizes of $n$ and $t$ for each test case are summarized as follows.

Test Case	$n$	$t$
1	$n=2\times 10$	$t=2$
2	$n=2\times {10}^3$	$t=0$
3		$t=3$
4	$n=2\times {10}^5$	$t=0$
5		$t=2$
6		$t=1$
7
8
9		$t=3$
10

Warning

The input and output requires 64-bit integers. If your calculations require operating on two 64-bit integers, be careful of whether the result will overflow.

Problem translated to English by Alex.