National Olympiad in Informatics, China, 2013

Little E really likes calligraphy. He heard that NOI2013 has started, and would like to give a calligraphic design of NOI to everyone.

Little E has one sheet of magical paper. The paper can be represented as a two-dimensional grid with ~n~ rows and ~m~ columns. We consider the coordinates of the bottom-left corner to be ~(1, 1)~ and the coordinates of the top-right corner to be ~(m, n)~. Each cell of the grid contains an integer "luckiness" value. Writing on a cell can increase everyone's luckiness. The overall luckiness just happens to be the sum of the luckiness values across all cells that have been written on. Now, you need to write the three letters N, O, and I onto the paper.

The three calligraphic letters are defined as follows:

1. The N is made up of some number ~(\ge 3)~ of rectangles which are parallel to the grid's axes. Let ~K~ be the number of rectangles (numbered from ~1~ to ~K~), then the ~i~-th rectangle's bottom-left corner will have coordinates ~(L_i, B_i)~, and its top-right corner will have coordinates ~(R_i, T_i)~. These values will satisfy:
   1. ~L_i \le R_i, B_i \le T_i~;
   2. For all ~1 < i \le K~, it will hold true that ~L_i = R_{i-1} + 1~;
   3. For all ~3 \le i < K~, it will hold true that ~B_{i-1} - 1 \le T_i \le T_{i-1}, B_i \le B_{i-1}~;
   4. ~B_2 > B_1, T_2 = T_1, B_{K-1} = B_K, T_{K-1} < T_K~.
2. The O is made up of a bigger rectangle ~A~, with a smaller rectangle ~B~ carved out of it. The two rectangles both have sides parallel to the grid's axes. Let ~(u, v)~ represent the coordinates of the bottom-left corner of rectangle ~A~, and ~W~ and ~H~ represent its width and height respectively. Then, the smaller rectangle ~B~ will have bottom-left corner at ~(u+1, v+1)~, a width of ~W-2~, and a height of ~H-2~. These values will satisfy:
   1. ~W \ge 3, H \ge 3~;
   2. ~u > R_K + 1~.
3. The I is made up of ~3~ rectangles with sides parallel to the grid's axes, numbered ~1~, ~2~, and ~3~ from bottom to top. Let ~(P_i, Q_i)~ represent the coordinates rectangle ~i~'s bottom-left corner, and ~(G_i, H_i)~ represent the coordinates of its top-right corner. These values will satisfy:
   1. ~P_i \le G_i, Q_i \le H_i~;
   2. ~P_1 = P_3 > u + W, G_1 = G_3~;
   3. ~Q_1 = H_1 = Q_2 - 1, H_2 + 1 = Q_3 = H_3~;
   4. ~P_1 < P_2 \le G_2 < G_1~;

The following depicts an example of a valid calligraphic design of the letters N, O, and I.

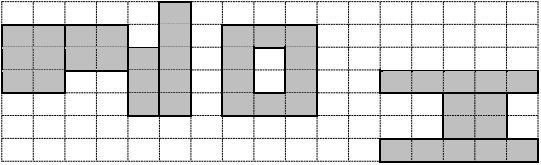
Also, shapes drawn in the design must not extend beyond the boundaries of the grid. Little E would like to determine the maximum possible luckiness that his design could produce.

Input Specification

The first line of input will contain two positive integers ~n~ and ~m~, respectively representing the number of rows and columns in the grid.
The next ~n~ lines will each contain ~m~ integers. The ~j~-th integer on line ~i+1~ of the input represents the luckiness value of the grid cell at ~(j, n-i+1)~.

Output Specification

Output a single integer ~T~, representing the maximum total luckiness that his design could produce.

Sample Input 1

3 13
1 1 -1 -1 1 -1 1 1 1 -1 1 1 1
1 -1 1 -1 1 -1 1 -1 1 -1 -1 1 -1
1 -1 -1 1 1 -1 1 1 1 -1 1 1 1

Sample Output 1

24

Explanation for Sample 1

Sample Input 2

3 13
-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1

Sample Output 2

-20

Explanation for Sample 2

The following is one optimal design. There also exist other optimal designs.

Constraints

Test Case	~n~	~m~	Range of Luckiness Values
~1~	~= 3~	~= 12~	~[-50, 50]~
~2~
~3~
~4~
~5~	~\le 10~	~\le 20~
~6~
~7~
~8~
~9~	~\le 150~	~\le 500~	~= 1~
~10~
~11~	~\le 80~	~\le 80~	~[-200, 200]~
~12~
~13~
~14~
~15~	~\le 150~	~\le 500~
~16~
~17~
~18~
~19~
~20~

All test cases satisfy ~n \ge 3~ and ~m \ge 12~.

Problem translated to English by Alex.