National Olympiad in Informatics, China, 2007

Recently, Alex has made shocking advances in the technique of counting spanning trees in undirected, connected graphs. He discovered:

• A cycle with $n$ nodes contains $n$ distinct spanning trees.
• A complete graph with $n$ nodes contains $n^{n-2}$ distinct spanning trees.

These two discoveries have made Alex ecstatic, so he would like to continue on his adventure of counting spanning trees. That is, he would like to be able to count the number of spanning trees in all kinds of different graphs.

One day, Alex is meeting up with his peers. Everyone sat in a circle around a big round table. After taking a look, Alex immediately recalls his spanning tree problem. If he considers each of his peers as a node and neighboring peers (nodes with a distance of $1$ between them) to be connected by an edge, then this becomes a cycle. However, Alex has already mastered calculations on cycles and is not really interested anymore. So, he changed the graph up a bit: Not only does he add an edge between neighboring peers, but he also adds an edge between pairs of peers who are separated by a single seat (nodes with a distance of $2$ between them). Now, he considers peers connected by a single edge to be adjacent, as depicted in the following figure.

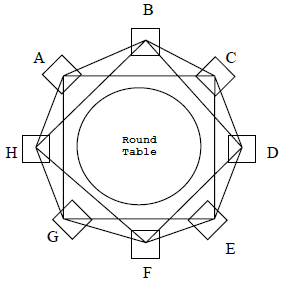
Alex has never tried counting spanning trees on this kind of graph before, however, he recalls his teacher explaining that there is a general method for counting the number of spanning trees on any type of graph. First, construct an $n\times n$ matrix $A=\{a_{ij}\}$ such that:

$${\displaystyle a_{ij}=\{\begin{array}{ll}{d}_i& i=j\\ -1& i\text{ and }j\text{ are adjacent}\\ 0& \text{otherwise}\end{array}}$$

where $d_i$ represents the degree of node $i$.

Let's construct the matrix $A$ corresponding to the graph of the round table as depicted above. To count the number of spanning trees, we only have to remove the last row and column of $A$, obtaining an $(n-1)\times (n-1)$ matrix which we shall call $B$. Computing the determinant of matrix $B$ will yield the number of spanning trees in the graph above.

$${\displaystyle A=\left[\begin{array}{cccccccc}4& -1& -1& 0& 0& 0& -1& -1\\ -1& 4& -1& -1& 0& 0& 0& -1\\ -1& -1& 4& -1& -1& 0& 0& 0\\ 0& -1& -1& 4& -1& -1& 0& 0\\ 0& 0& -1& -1& 4& -1& -1& 0\\ 0& 0& 0& -1& -1& 4& -1& -1\\ -1& 0& 0& 0& -1& -1& 4& -1\\ -1& -1& 0& 0& 0& -1& -1& 4\end{array}\right]B=\left[\begin{array}{ccccccc}4& -1& -1& 0& 0& 0& -1\\ -1& 4& -1& -1& 0& 0& 0\\ -1& -1& 4& -1& -1& 0& 0\\ 0& -1& -1& 4& -1& -1& 0\\ 0& 0& -1& -1& 4& -1& -1\\ 0& 0& 0& -1& -1& 4& -1\\ -1& 0& 0& 0& -1& -1& 4\end{array}\right]}$$

Therefore the number of spanning trees in this graph is $|B|=3528$. Alex noticed that using the general method, calculations are very complex and tedious. Yet, he cannot find any other formulas that are simpler than this. So, he simplified the graph. At some place, he broke apart the circle around the table. This way, his peers form a chain of nodes, where an edge exists between all pairs of nodes with a distance of $1$ or a distance of $2$ between them. The case for $8$ nodes is depicted below:

This way, the total number of spanning trees is reduced by a great amount. Alex just thinks and thinks, until the entire meeting is over. Finally, he comes up with an efficient method to count the number of spanning trees in this graph. However, if he also decides to join nodes with a distance of $3$, then once again he will not know how to find the answer efficiently. Please help Alex count the number of spanning trees in these types of graphs!

Input Specification

The input contains two integers $k$ and $n$, separated by a space. $k$ means that all nodes with a distance no greater than $k$ are to be linked by an edge in the graph. $n$ indicates that there are $n$ total nodes.

Output Specification

Output a single integer, the number of spanning trees in the graph. Since the answer can be rather large, you are required to output the answer modulo $65521$.

Sample Input

3 5

Sample Output

75

Explanation

The graph for the sample is depicted below:

$${\displaystyle A=\left[\begin{array}{ccccc}3& -1& -1& -1& 0\\ -1& 4& -1& -1& -1\\ -1& -1& 4& -1& -1\\ -1& -1& -1& 4& -1\\ 0& -1& -1& -1& 3\end{array}\right]B=\left[\begin{array}{cccc}3& -1& -1& -1\\ -1& 4& -1& -1\\ -1& -1& 4& -1\\ -1& -1& -1& 4\end{array}\right]}$$

$${\displaystyle |B|=75}$$

Constraints

For all the test cases, $2\le k\le n$.

Test Case	Range of $k$	Range of $n$	Test Case	Range of $k$	Range of $n$
$1$	$k=2$	$n\le 10$	$6$	$k\le 5$	$n\le 100$
$2$	$k=3$	$n=5$	$7$	$k\le 3$	$n\le 2000$
$3$	$k=4$	$n\le 10$	$8$	$k\le 5$	$n\le 10000$
$4$	$k=5$	$n=10$	$9$	$k\le 3$	$n\le {10}^{15}$
$5$	$k\le 3$	$n\le 100$	$10$	$k\le 5$	$n\le {10}^{15}$

Hints

One method to compute the determinant is to first let $\alpha (P)$ represent the number of inversions in the sequence $P$. Then, the determinant of $B$ is calculated using the formula:

$${\displaystyle |B|=\sum _{P=p_1,p_2,\dots ,p_n\text{ is a permutation of 1 to }n}(-1{)}^{\alpha (P)}\prod _{j=1}^n{b}_{i,p_i}}$$

If $B=\left[\begin{array}{ccc}1& 2& 3\\ 4& 5& 6\\ 7& 8& 0\end{array}\right]$, then the calculations are as follows:

$P$	$\alpha (P)$	$b_{1,p_1}$	$b_{2,p_2}$	$b_{3,p_3}$	$(-1{)}^{\alpha (P)}\prod _{j=1}^n{b}_{i,p_i}$
$1,2,3$	$0$	$1$	$5$	$0$	$0$
$1,3,2$	$1$	$1$	$6$	$8$	$-48$
$2,1,3$	$1$	$2$	$4$	$0$	$0$
$2,3,1$	$2$	$2$	$6$	$7$	$84$
$3,1,2$	$2$	$3$	$4$	$8$	$96$
$3,2,1$	$3$	$3$	$5$	$7$	$-105$

Therefore the determinant of $B$ is $0-48+0+84+96-105=27$.

Problem translated to English by Alex.