NOI '06 P3 - Millennium Worm
View as PDFNational Olympiad in Informatics, China, 2006
The millennium worm is an ancient life form. Since tens of millions of years ago, the millennium worm has already vanished from the surface of the earth. As a result, humans know very little about them. Archaeologists recently started to gain interest in the matter, for a number of precious millennium worm fossils have recently been discovered. These fossils have preserved virtually the entire form of the millennium worm.
Theoretical scientists have used these fossils to determine a morphological model of the millennium worm, and further concluded that the millennium worm is the ancestor of the centipede! However, scientist J has found some discrepancies between practicality and theory. After carefully researching hundreds of millennium worm fossils, he has discovered that the majority of millennium worm structures do not fully correspond to the theoretical model. Just how could this be? Theoretical scientist K points out that while the millennium worm is in fossil form, it may experience various types of changes. Even the subtlest change can result in it being inconsistent with the model.
So, a new problem is born in the face of scientists: predict for a given
fossilized millennium worm how different it is from the theoretical
model. Generally speaking, for a given millennium worm fossil shape ,
the problem is to find a shape
that fits the theoretical model, such
that
is the most likely shape to turn into shape
when it was being
fossilized.
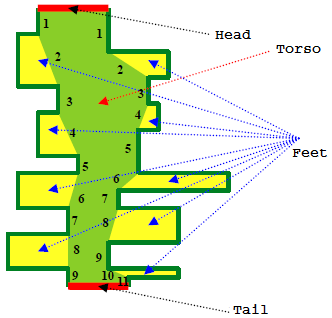
The "millennium worm physical features model" as proposed by theoretical scientists is as follows (depicted in the left figure): its body consists of the head, tail, torso, and feet as its four major components.
- The head and tail are indicated by a pair of parallel line
segments. We shall consider the direction parallel to the head and
tail the
direction, and the direction perpendicular to that, the
direction.
- The head and tail are joined in-between by two non-intersecting
folded line segments. These lines, along with the head and tail,
together enclose a region known as the torso. The folded line
segments satisfy the following conditions: each folded angle is
either an obtuse angle or a straight angle, there must be an odd
number of line segments, and there must be an odd number of line
segments perpendicular to the
direction from top to bottom.
- Counting from top to bottom, the torso at each even-numbered line
segment of the folded line segments has a single foot growing
out of one side. The foot has its top and bottom sides parallel
to the
direction, and is either trapezoidal or rectangular. The side facing away from the torso is perpendicular to the
direction.
Note: The shape of its feet cannot regress to a triangle (thus the length of each foot's base is greater than zero), and the number of feet on each side of the torso may be different. (As shown in the given figure, there are 4 feet on the left side, and 5 feet on the right side.)
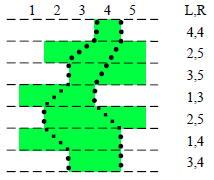
As it can be seen, in the Cartesian coordinate system, the
borders of the solid region formed by the torso and feet are each
parallel or perpendicular to the axes. For simplicity, let us assume
that the lengths of each of these borderlines are positive integers.
Thus, we can believe that the body of each millennium worm is
representable using a bunch of unit squares. Each unit is uniquely
defined by some coordinates
. Let the distance between the
head and tail be
; then we can use
integers to describe one
millennium worm
(as shown in the figure to the right): Split
up into
strips of width 1 parallel to the
direction. Let the leftmost
unit of each strip have the
-coordinate of
, and the rightmost
unit have the
-coordinate of
. Then, we can use
to specify a single
millennium worm.
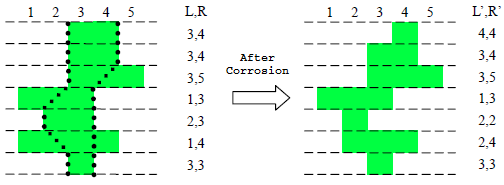
Due to years of erosion, in the actual fossil, the shape of the millennium worm does not satisfy the specifications of the theoretical model. Sections of its body in some cells have already been corroded by certain minerals.
Geologists, physicists, and biologists have worked together to conclude that:
- Corrosion happens with individual cells; only whole grid units can be corroded.
- Corrosion happens in steps; only one cell can be corroded at every step.
- If the body is disconnected after removing a cell, then of course this cell cannot be corroded.
- If neither a cell's left neighbor nor its right neighbor has been corroded, then this cell cannot currently be corroded.
- Cells neighboring the head cannot all be corroded. Cells neighboring the tail cannot all be corroded.
If we satisfy the five conditions above, we can still use
to specify the conditions
of a fossilized millennium worm, where
. For
example, examine the following figure:
Your task is, given the specifications of a fossilized millennium worm
, determine specifications
which
satisfy the theoretical millennium worm description, such that
can
be transformed into
through the corrosion process, and that the cost
to transform
to
(i.e. the number of cells that need to be
corroded) is minimized. Output this smallest number of steps.
Input Specification
The first line of input contains a single integer .
For the following lines, each line contains two integers. The
-th
line of these lines contains two integers
, and
,
separated by a single space.
It is guaranteed that the input data will be valid.
Output Specification
Output a single line containing a single integer, representing the minimum cost.
Sample Input
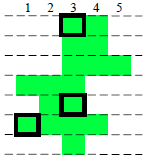
7
4 4
3 4
3 5
1 3
2 2
2 4
3 3Sample Output
3Explanation
See figure below.
Constraints
For all test cases, ,
.
| Test Case | ||
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
| 9 | ||
| 10 |
Problem translated to English by .
Comments