NOI '05 P6 - Lemon Tree Under the Moon - Olympiads Online Judge

NOI '05 P6 - Lemon Tree Under the Moon

View as PDF

Submit solution

All submissions

Best submissions

Points: 30

Time limit: 0.18s

Memory limit: 256M

Problem types

National Olympiad in Informatics, China, 2005

Li Zhe really really likes his lemon tree, especially on silent nights. When the sky has a crescent moon gently casting light onto the scenery on earth, he feels the need to sit leisurely under the lemon tree which he had planted with his own hands, pondering the philosophies of life.

Li Zhe is a child who enjoys thinking. When he noticed that the shadow casted by the moonlight hitting the lemon tree is extra clear on the ground, he immediately comes up with a question: how large is the area of the tree's shadow?

Li Zhe knows that it is very difficult to directly measure area. Since he is very familiar with the shape of the lemon tree, he would like to use a geometrical method to calculate it. Thus, he has come up with a simplified method.

Li Zhe has split the entire lemon tree into $n$ ~n~ layers, labeled $1, 2, \dots, n$ ~1, 2, \dots, n~ from bottom to top. From layer $1$ ~1~ to layer $n-1$ ~n-1~, each layer is disk-shaped (*), with the exception of layer $n$ ~n~ (the uppermost layer), which is conical. Regarding the disks, the upper and lower surfaces are parallel to each other. Regarding any two neighboring disks, the bottom surface of the upper disk is always completely touching the top surface of the lower disk, and vice versa. The bottom surface of the cone at layer $n$ ~n~ (the uppermost layer) is the top surface of the disk at layer $n-1$ ~n-1~. The circular centers of all of the surfaces (including the treetop) are aligned along a straight line that is perpendicular to the ground. Li Zhe knows that the heights of all the layers are $h_1, h_2, \dots, h_n$ ~h_1, h_2, \dots, h_n~, that the distance from the bottom surface of layer $1$ ~1~ to the ground is $h_0$ ~h_0~, and that the radius of the bottom surface of each layer is $r_1, r_2, \dots, r_n$ ~r_1, r_2, \dots, r_n~. Li Zhe has used a familiar method to determine the angle $alpha$ ~alpha~ of the moonlight's rays against the surface of the ground.

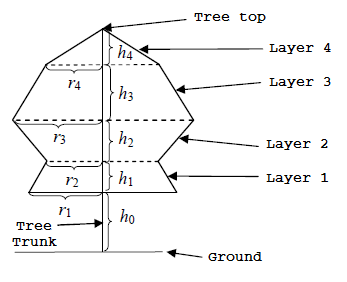
Figure 1. Cross-section of the lemon tree

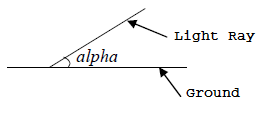
Figure 2. Depiction of moonlight ray angles

To simplify calculations, assume that light rays are parallel to each other, the ground is perfectly level, and the area of the shadow produced by the tree trunk is negligible. Li Zhe obviously knows how to find the answer, but he wishes for you to also try your hands.

Input Specification

Line $1$ ~1~ of input contains the integer $n$ ~n~ and the real number $alpha$ ~alpha~, representing the number of layers in the lemon tree and the angle with which the moonlight strikes the ground.
Line $2$ ~2~ contains $n+1$ ~n+1~ real numbers $h_0, h_1, h_2, \dots, h_n$ ~h_0, h_1, h_2, \dots, h_n~, representing the heights of all the layers.
Line $3$ ~3~ contains $n$ ~n~ real numbers $r_1, r_2, \dots, r_n$ ~r_1, r_2, \dots, r_n~, representing the radii of the bottom surfaces of all the layers.
Adjacent values on the same line in the input will always be separated by a single space.
Real values in the input will have between $1$ ~1~ and $10$ ~10~ significant digits, inclusive.

Output Specification

The output should contain $1$ ~1~ real number – the area of the tree's shadow, rounded and displayed to two places after the decimal.

Sample Input

2 0.7853981633
10.0 10.00 10.00
4.00 5.00

Sample Output

171.97

Constraints

$1 \le n \le 500$ ~1 \le n \le 500~; $0.3 < alpha < \frac \pi 2$ ~0.3 < alpha < \frac \pi 2~; $0 < h_i \le 100$ ~0 < h_i \le 100~; $0 < r_i \le 100$ ~0 < r_i \le 100~.
In test cases worth $10\%$ ~10\%~ of points, $n \le 1$ ~n \le 1~.
In test cases worth $30\%$ ~30\%~ of points, $n \le 2$ ~n \le 2~.
In test cases worth $60\%$ ~60\%~ of points, $n \le 20$ ~n \le 20~.
In test cases worth $100\%$ ~100\%~ of points, $n \le 500$ ~n \le 500~.

* Note from translator: Layers $1$ ~1~ to $n-1$ ~n-1~ are more accurately described as truncated cone-shaped.

Problem translated to English by Alex.

Comments

1

Alb11747 commented on Sept. 25, 2020, 8:42 p.m.

What am I missing from my program? Is my angle calculation correct?

1

Render_Main commented on Sept. 25, 2020, 10:55 p.m. ← edit 2 →

Your program handles the angle correctly. You did wrong in the area calculation.

Each (except the last) layer of the tree is truncated cone-shaped. A possible shape of the tree's shadow may look like this:

To solve this problem, you need to find the area of the shaded region, which can be done analytically using the scan-line algorithm or using a numerical integration method like the Simpson's rule. The implementation is left as an exercise for you.

Edit 2021-01-30: additional test cases are added to the problem and numerical solutions no longer pass.

0

Alb11747 commented on Oct. 3, 2020, 3:33 a.m.

Is the problem accuracy now or am I just completely off?