National Olympiad in Informatics, China, 2002

Yuan Yuan is getting tired of the traditional game of Tetris, so she has decided to create a new set of rules. The game takes place on an infinitely-tall grid of ~N~ ~(1 \le N \le 1500)~ columns, where the columns of the grid from left to right are labeled from ~1~ to ~N~. In this game, the player uses the ~19~ types of tiles depicted in figure 1. Every such tile is made up of exactly four smaller squares. The picture contains the numberings of the tiles ~T~ ~(1 \le T \le 19)~.

The rules of the game are as follows:

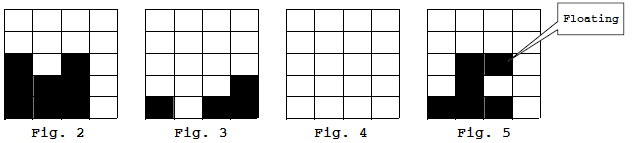
1. To describe the status of the grid: Every possible state of the grid in the game is described using the number of consecutive squares in each column. For example in figure 2, the grid contains ~N = 4~ columns. Column ~1~ contains ~3~ small squares. Column ~2~ contains two small squares. Column ~3~ contains ~3~ small squares. Column ~4~ contains ~0~ small squares. Therefore, we can use the ~4~-tuple ~(3, 2, 3, 0)~ to describe this grid state.
2. The game initially selects a tile ~T~ ~(1 \le T \le 19)~ and drops it into a specified column ~C~ ~(1 \le C \le N)~. The command is described by the pair ~(T, C)~. That is, the leftmost square(s) of tile number ~T~ is lined up with column ~C~ and dropped. An example is depicted in figure 2, where tile number ~T = 1~ is placed in column ~C = 4~, representing the command ~(1, 4)~. The tile continues to fall until it reaches the bottom of the grid, immediately creating the game state ~(3, 2, 3, 4)~. However since the bottom two rows are filled completely, the rules will make these two rows automatically vanish, reaching the state depicted in figure 3, denoted by ~(1, 0, 1, 2)~.
3. The game ends when the number of squares in all the columns is ~0~. For example, when tile number ~9~ is selected and dropped in the leftmost column of the grid in figure 3 using the command ~(9, 1)~, the immediate game state would become ~(2, 2, 2, 2)~. The two entire rows vanish after being filled, resulting in the game state ~(0, 0, 0, 0)~, finally successfully ending the game.
4. The rules require that tiles never occupy regions outside of the bounds of the grid. For example, in figure 2 where ~N = 4~, the command ~(18, 4)~ will be out of bounds.
5. The rules require that no tiles may produce "floating" squares. A floating square is a square positioned such that not all of the squares in its column are consecutive. Figure 5 is one such situation. For example, in the grid for figure 2, the commands ~(2, 1)~, ~(17, 2)~, and ~(10, 3)~ are all illegal.

Although the ability to pick which tiles drop greatly simplifies the game, completely getting rid of all the squares still remains a very annoying task. Would you like to try?

Input Specification

The first line of input contains an integer ~N~, the number of columns. The second line contains ~N~ integers, representing the initial state of the grid. Each integer on this line represents the number of consecutive squares in the corresponding column.

Output Specification

The output should contain many lines of commands. Each line should contain two integers ~T~ and ~C~, separated by a space. It is guaranteed that there is a solution, although not necessarily unique. You may output any such solution.

Sample Input

4
3 2 3 0

Sample Output

1 4
9 1

Scoring

For each test case, your score out of ~10~ will be:

• ~0~, if your output is incorrect or the number of commands exceeds ~1\,000\,000~.
• ~7~, if your output is correct but the number of commands exceeds ~100\,000~.
• ~10~, if your output is correct and the number of commands does not exceed ~100\,000~.

Problem translated to English by Alex.