Robert is designing a new computer game. The game involves one hero, $n$ opponents and $n+1$ dungeons. The opponents are numbered from $0$ to $n-1$ and the dungeons are numbered from $0$ to $n$. Opponent $i$ $(0\le i\le n-1)$ is located in dungeon $i$ and has strength $s[i]$. There is no opponent in dungeon $n$.

The hero starts off entering dungeon $x$, with strength $z$. Every time the hero enters any dungeon $i$ $(0\le i\le n-1)$, they confront opponent $i$, and one of the following occurs:

• If the hero's strength is greater than or equal to the opponent's strength $s[i]$, the hero wins. This causes the hero's strength to increase by $s[i]$ $(s[i]\ge 1)$. In this case the hero enters dungeon $w[i]$ next $(w[i]>i)$.
• Otherwise, the hero loses. This causes the hero's strength to increase by $p[i]$ $(p[i]\ge 1)$. In this case the hero enters dungeon $l[i]$ next.

Note $p[i]$ may be less than, equal to, or greater than $s[i]$. Also, $l[i]$ may be less than, equal to, or greater than $i$. Regardless of the outcome of the confrontation, the opponent remains in dungeon $i$ and maintains strength $s[i]$.

The game ends when the hero enters dungeon $n$. One can show that the game ends after a finite number of confrontations, regardless of the hero's starting dungeon and strength.

Robert asked you to test his game by running $q$ simulations. For each simulation, Robert defines a starting dungeon $x$ and starting strength $z$. Your task is to find out, for each simulation, the hero's strength when the game ends.

Implementation Details

You should implement the following procedures:

void init(int n, std::vector<int> s, std::vector<int> p, std::vector<int> w, std::vector<int> l)

• $n$: number of opponents.
• $s$, $p$, $w$, $l$: arrays of length $n$. For $0\le i\le n-1$:
  • $s[i]$ is the strength of the opponent $i$. It is also the strength gained by the hero after winning against opponent $i$.
  • $p[i]$ is the strength gained by the hero after losing against opponent $i$.
  • $w[i]$ is the dungeon the hero enters after winning against opponent $i$.
  • $l[i]$ is the dungeon the hero enters after losing against opponent $i$.
• This procedure is called exactly once, before any calls to simulate (see below).

long long simulate(int x, int z)

• $x$: the dungeon the hero enters first.
• $z$: the hero's starting strength.
• This procedure should return the hero's strength when the game ends, assuming the hero starts the game by entering dungeon $x$, having strength $z$.
• The procedure is called exactly $q$ times.

Examples

Consider the following call:

init(3, {2, 6, 9}, {3, 1, 2}, {2, 2, 3}, {1, 0, 1})

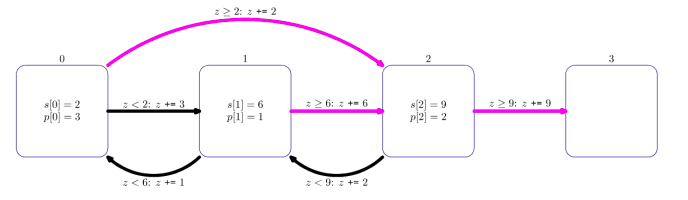
The diagram above illustrates this call. Each square shows a dungeon. For dungeons $0$, $1$ and $2$, the values $s[i]$ and $p[i]$ are indicated inside the squares. Magenta arrows indicate where the hero moves after winning a confrontation, while black arrows indicate where the hero moves after losing.

Let's say the grader calls simulate(0, 1).

The game proceeds as follows:

Dungeon	Hero's strength before confrontation	Result
$0$	$1$	Lose
$1$	$4$	Lose
$0$	$5$	Win
$2$	$7$	Lose
$1$	$9$	Win
$2$	$15$	Win
$3$	$24$	Game ends

As such, the procedure should return $24$.

Let's say the grader calls simulate(2, 3).

The game proceeds as follows:

Dungeon	Hero's strength before confrontation	Result
$2$	$3$	Lose
$1$	$5$	Lose
$0$	$6$	Win
$2$	$8$	Lose
$1$	$10$	Win
$2$	$16$	Win
$3$	$25$	Game ends

As such, the procedure should return $25$.

Constraints

• $1\le n\le 400000$
• $1\le q\le 50000$
• $1\le s[i],p[i]\le {10}^7$ (for all $0\le i\le n-1$)
• $0\le l[i],w[i]\le n$ (for all $0\le i\le n-1$)
• $w[i]>i$ (for all $0\le i\le n-1$)
• $0\le x\le n-1$
• $1\le z\le {10}^7$

Subtasks

1. ($11$ points) $n\le 50000,q\le 100,s[i],p[i]\le 10000$ (for all $0\le i\le n-1$)
2. ($26$ points) $s[i]=p[i]$ (for all $0\le i\le n-1$)
3. ($13$ points) $n\le 50000$, all opponents have the same strength, in other words, $s[i]=s[j]$ for all $0\le i,j\le n-1$.
4. ($12$ points) $n\le 50000$, there are at most $5$ distinct values among all values of $s[i]$.
5. ($27$ points) $n\le 50000$
6. ($11$ points) No additional constraints.

Sample Grader

The sample grader reads the input in the following format:

• line $1$: $nq$
• line $2$: $s[0]s[1]\dots s[n-1]$
• line $3$: $p[0]p[1]\dots p[n-1]$
• line $4$: $w[0]w[1]\dots w[n-1]$
• line $5$: $l[0]l[1]\dots l[n-1]$
• line $6+i$ $(0\le i\le q-1)$: $xz$ for the $i$-th call to simulate.

The sample grader prints your answers in the following format:

• line $1+i$ $(0\le i\le q-1)$: the return value of the $i$-th call to simulate.

Attachment Package

The sample grader and sample test cases are available here: dungeons.zip.