Although the employees are already assigned numbers in the input, the numbers can be reassigned in a way that makes them more useful. The supervisor relationships clearly organize the employees into a tree. Assign the new employee numbers in a pre-order walk of the tree³. Figure 1 shows an example of such a numbering.

³ A pre-order walk of a tree first processes the root of that tree, then recursively processes each sub-tree in turn.

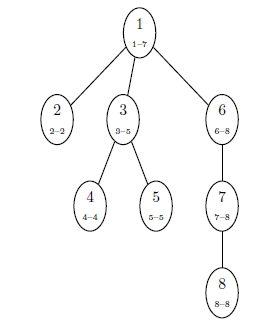
Figure 1: An example of numbering employees by a pre-order walk. The bottom numbers indicate the range of employee numbers in each sub-tree.

A useful property of this numbering is that all the employees in a sub-tree have sequential numbers. For a given employee ~e~, let ~[e]~ be the range of employee numbers managed by ~e~. Notice that for a region, we can construct an ordered array of all the interval end-points for that region, and a list of all employees in that region. This can be done during the assignment of numbers in linear time.

Now let us consider how to answer queries ~(r_1, r_2)~. Let the sizes of the regions be ~S_1~ and ~S_2~ respectively. Given this data structure, a natural solution is to consider every pair of employees ~(e_1, e_2)~ from these regions and check whether ~e_2~ lies in the interval ~[e_1]~. However, this will take ~\mathcal O(S_1 S_2)~ time per query, which we can improve upon.

The interval end-points for region ~r_1~ divide the integers into contiguous blocks. All employees in the same block have the same managers from ~r_1~, and we can precompute the number of such managers for each such block. This gives us a faster way to answer queries. Rather than comparing every employee in ~r_2~ with every block for ~r_1~, we can observe that both are ordered by employee ID. Thus, one can maintain an index into each list, and in each step advance whichever index is lagging behind the other. Since each index traverses a list once, this takes ~\mathcal O(S_1+S_2)~ time.

Using just this query mechanism can still take ~\mathcal O(NQ)~ time, because all the queries might involve large regions. However, it is sufficient to earn the points for the tests where no region has more than ~500~ employees.

Precomputing queries

In the query algorithm above, it is also possible to replace the list of employees in ~r_2~ with the entire list of employees, and thus compute the answer to all queries for a particular ~r_1~. This still requires only a single pass over the blocks for ~r_1~, so it takes ~\mathcal O(N)~ time to produce all the answers for a particular ~r_1~. Similarly, one can iterate over all interval end-points while fixing ~r_2~, giving all answers for a particular ~r_2~.

This allows all possible queries to be pre-computed in ~\mathcal O(RN)~ time and ~\mathcal O(R^2)~ memory. This is sufficient to earn the points for the tests where ~R \le 500~.

This algorithm is too slow and uses too much memory to solve all the tests. However, it is not necessary to precompute all answers, just the most expensive ones. We will precompute the answers involving regions with size at least ~c~. There are obviously at most ~N/c~ such regions, so this will take ~\mathcal O(N^2/c)~ time and ~\mathcal O(RN/c)~ memory. The remaining queries involve only small regions, so they can be answered in ~\mathcal O(Qc)~ time. Choosing ~c = \sqrt N~ gives ~\mathcal O((N+Q) \sqrt N)~ time and ~\mathcal O(R \sqrt N)~ memory, which is sufficient for a full score.

Caching queries

As an alternative to precomputation, one can cache the results of all queries, and take the answer from the cache if the same query is made again. Let ~Q'~ be the number of unique queries. The cost of maintaining the query cache depends on the data structure used; a balanced binary tree gives ~\mathcal O(Q \log N)~ overhead for this.

Combining the cache with the ~\mathcal O(S_1+S_2)~ algorithm is sufficient to achieve the points for tests that have either no more than ~500~ employees per region (because this is the case even without the cache), as well as the cases with no more than ~500~ regions (since the total cost of all distinct queries together is ~\mathcal O(RN)~).

To achieve a full score with a cache rather than precomputation, one must use a better method for answering queries. Suppose we have a block in ~r_1~, and wish to find all matching employees from ~r_2~. While we have previously relied on a linear walk over the employees from ~r_2~, we can instead use a binary search to find the start and end of the range in ~\mathcal O(\log S_2)~ time. This allows the entire query to be answered in ~\mathcal O(S_1 \log S_2)~ time. A similar transformation (binary searching the blocks for each employee in ~r_2~) gives ~\mathcal O(S_2 \log S_1)~ time for each query.

Now when answering each query, choose the best out of the ~\mathcal O(S_1 \log S_2)~, ~\mathcal O(S_2 \log S_1)~ and ~\mathcal O(S_1+S_2)~ query mechanisms. To establish an upper bound on run-time, we will make assumptions about which method is chosen to answer particular types of queries.

Again, divide the problem into large regions with at least ~c~ employees and the rest. For queries involving one of the large regions, use the ~\mathcal O(A \log B)~ algorithm (where ~A~ and ~B~ are respectively the smaller and larger of ~S_1~ and ~S_2~). The caching of queries ensures that this contributes no more than ~\mathcal O(N^2 \log N/c)~ time. For the remaining queries, use an ~\mathcal O(S_1+S_2)~ algorithm. The smaller regions have at most ~c~ employees, so this contributes ~\mathcal O(Qc)~ time.

The optimal value of ~c~ occurs when the two parts account for equal time. Solving for this optimal ~c~ gives a bound of ~\mathcal O(N \sqrt{Q' \log N})~ for answering non-duplicate queries; combined with the cost for the query cache, this gives an algorithm with time complexity ~\mathcal O(N \sqrt{Q' \log N} + Q \log N)~ and memory complexity ~\mathcal O(N+Q')~.

The time bound is marginally worse than for the first solution, but in practical terms this solution runs at about the same speed and uses significantly less memory.