At any moment during the cutting, we have a set of independent sub-problems — blocks of chocolate. If we find the optimal solution for each of the blocks, together we get the optimal solution for the whole chocolate. This clearly hints at a dynamic programming solution.

Each sub-problem we may encounter corresponds to a rectangular part of the chocolate, and it can be described by four coordinates: specifically, two $x$ and two $y$ coordinates — the coordinates of its upper left and lower right corner. Hence we have $\mathcal{O}(N^4)$ sub-problems to solve.

Now to solve a given sub-problem, we have to try all possible cuts. There are $\mathcal{O}(N)$ possible cuts to try — at most $N-1$ horizontal and $N-1$ vertical ones. Each possible cut gives us two new, smaller sub-problems we solve recursively. Obviously, the recursion stops as soon as we reach a $1\times 1$ block.

Assume that someone has given us a function $S(x_1,y_1,x_2,y_2)$ that returns the number of raisins in the rectangle given by coordinates $(x_1,y_1)$ and $(x_2,y_2)$ in constant time.

Using this function we can solve the entire problem in $\mathcal{O}(N^5)$. We will use recursion with memoization. Given any of the $\mathcal{O}(N^4)$ sub-problems, first check the memoization table to see whether we have computed it already. If yes, simply return the previously computed value. Otherwise, proceed as follows: The cost of the first cut is $S(x_1,y_1,x_2,y_2)$, which we have supposed can be computed in $\mathcal{O}(1)$ time. For each possible placement of the first cut, recursively determine the cost of the remaining cuts in each sub-problem, and pick the optimal choice, storing the answer in the memoization table.

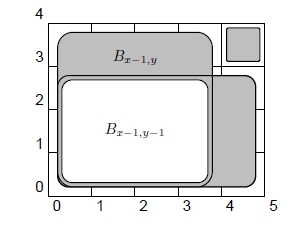
We are only missing one piece of the puzzle: the function $S$. All possible values can easily be precomputed in $\mathcal{O}(N^4)$ and stored in an array.

Alternatively, we can use two-dimensional prefix sums: let $A$ be the input array, and let $B_{x,y}=\sum _{i<x}\sum _{j<y}{A}_{i,j}$. The values $B$ are called two-dimensional prefix sums. They can be computed using the formula:

$${\displaystyle \mathrm{\forall }x,y>0:B_{x,y}=B_{x-1,y}+B_{x,y-1}-B_{x-1,y-1}+A_{x-1,y-1}}$$

Having the two-dimensional prefix sums, we can compute the sum in any rectangle, using a similar formula. The sum in the rectangle with corners $(x_1,y_1)$ and $(x_2,y_2)$ is:

$${\displaystyle S(x_1,y_1,x_2,y_2)=B_{x_2,y_2}-B_{x_1,y_2}-B_{x_2,y_1}+B_{x_1,y_1}}$$