Editorial for IOI '04 P6 - Empodia
Submitting an official solution before solving the problem yourself is a bannable offence.
Signed permutations are important in the study of DNA sequences [Ber01].
For each framed interval the following hold:
Fact 1: The starting () and finishing (
) point of a framed interval
are related with the following equation:
Fact 2: All values in the interior points of a framed interval are distinct and cover the entire interval exactly once.
Simple
A simple algorithm is the following. For each element of the sequence, one exhaustively seeks for framed intervals of length
(
) starting at element
, where
is the number of elements contained in the sequence
. For each pair
the corresponding length induces, someone inspects whether Fact 1 holds or not. If it does, then according to Fact 2 one must verify that all elements that lie in between are proper so that this interval is in fact a framed interval. We have
pairs
, and for each interval these pairs induce, we require
time to verify that this is a framed interval whenever Fact 1 holds. Thus, this part of the algorithm takes
time. During this part of the algorithm one keeps track of candidate hurdles starting at index
. Of course there is no need to keep track all of
framed intervals that might exist starting at index
, since all framed intervals that don't have minimum length can not be hurdles.
Moreover, according to our definition of hurdles, the algorithm requires another part so as to eliminate all those framed intervals that contain shorter framed intervals starting at different points. At this final part of the algorithm we have candidate hurdles. For each one of them one can verify in
time if another candidate hurdle is contained and decide whether this candidate hurdle is really a hurdle or not. This step of the algorithm takes
time.
As a result, the entire algorithm takes time.
Clever
Fact 3: The element with the minimum value in a hurdle is always the starting point of the hurdle.
Fact 4: The element with the maximum value in a hurdle is always the finishing point of the hurdle.
Crucial observation: An important observation for the proposed algorithm is stated by the following lemma:
Lemma 2.1 The endpoint(s) of a hurdle can not be in the interior of another hurdle.
Proof
Case 1: Both endpoints of a hurdle lie in the interior of another hurdle. Then obviously according to definition, one of the above framed intervals can not be a hurdle, which is a contradiction.
Case 2: Only one endpoint of a hurdle lies in the interior of another hurdle.
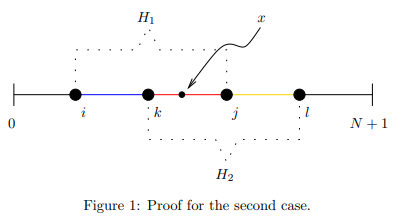
Suppose for the purpose of contradiction that a hurdle
has its starting point
in the interior of another hurdle
, a situation like the one shown in Figure 1. Then, based on the preceding facts we have:
since the
element is an interior point of hurdle
and
element is an interior point of hurdle
. Now pick an element with index
at random such that
. Obviously, this element belongs to hurdle
, so
. Moreover,
belongs to hurdle
, so
. In other words, every element with index
, such that
, implies that:
Finally, there is no other element
that implies (3) outside of the interval
, since if it were, then either hurdle
would not be a hurdle, or
. As a result, all intermediate values lie in this interval (shown with red line) and as a consequence we have a framed interval. But this is a contradiction to our assumption that intervals
and
form two different hurdles. This completes the proof.
Note: In fact, in the above case we can prove something even stronger. Since all elements in the interval imply equation (3), all elements in the interval
(blue line) imply that this region is also a framed interval since they belong to framed interval
. Finally, all the elements in the interval
(yellow line) imply that this region is also a framed interval, since they belong to framed interval
.
So, a better way to handle this problem is to find a "most suitable" candidate framed interval for each element . This can be achieved by scanning sequentially the elements of the given sequence from left to right and at the same time remembering the maximum value (
) found so far. Now, if someone finds an element
that has value
and at the same time Fact 1 is satisfied, it is easy to see that this implies the end of a framed interval. Since we have
elements to check and for each one of them we have
elements to scan, it is straightforward that in order to find all candidate framed intervals takes
time. On the following we present the algorithm in pseudocode assuming that the elements of the sequence are given in array
SEQ. The algorithm returns array FRAMED, where it is stored the length of a candidate hurdle starting at position .
Clever_Candidate_Enumeration(SEQ[])
for i ← 0 to N + 1
FRAMED[i] ← nil
for i ← 0 to N
max ← SEQ[i]
for k ← 1 to N + 1 - i
if ((SEQ[i + k] = SEQ[i] + k) AND (SEQ[i + k] = max + 1))
FRAMED[i] ← k + 1
else if (SEQ[i + k] < SEQ[i])
break
else if (SEQ[i + k] > max)
max ← SEQ[i + k]
return FRAMEDAs in the previous algorithm, we can perform the elimination of false alerts in time.
Elimination of false alerts in linear time
Based on the preceding lemma one can easily decide which of the candidate hurdles are in fact hurdles and not false alerts in linear time. One must keep track of the length of each candidate hurdle at its starting position in an array FRAMED. We say that a candidate hurdle is active if we examine elements in the interior of the hurdle.
The idea is the following. One scans sequentially the array FRAMED, and if he encounters a starting position of a candidate hurdle while a candidate hurdle
is active, then case 1 of lemma 2.1 must apply because the candidate hurdle
is a framed interval of minimum length starting at the starting position of candidate hurdle
. This process requires no more than
queries on array
FRAMED and as a result its running time is . The elimination algorithm is given with the following pseudocode:
Linear_Elimination(FRAMED[])
i ← 0
while (i < N + 1)
if (FRAMED[i] = nil)
k ← i + 1
while (k < FRAMED[i] + i - 1)
if (FRAMED[k] = nil)
FRAMED[i] ← nil
break
else k ← k + 1
i ← k - 1
else i ← i + 1
return FRAMEDFinally, either way we choose to eliminate false alerts, this algorithm has running time .
Advanced
This problem can be solved in superlinear [BH96] and linear (
) [BMY01] time if someone uses graphs. These results come from one of the most exciting areas in computer science in the last decade which was pioneered by Hannenhalli and Pevzner [HP95] and have rather simple implementations.
A detailed treatment of the field that inspired this problem can be found at [Sie01].
References
[Ber01] Anne Bergeron. A Very Elementary Presentation of the Hannenhalli-Pevzner Theory. CPM 2001 - Lecture Notes in Computer Science, 2089:106–117, April 19 2001.
[BH96] Piotr Berman and Sridhar Hannenhalli. Fast Sorting by Reversal. Proceedings of the 7th Annual Symposium on Combinatorial Pattern Matching, pages 168–185, 1996.
[BMY01] Bader, Moret, and Yan. A Linear-Time Algorithm for Computing Inversion Distance between Signed Permutations with an Experimental Study. In Lecture Notes in Computer Science, editor, WADS: 7th Workshop on Algorithms and Data Structures, volume 2125, pages 365–376, 2001.
[HP95] Sridhar Hannenhalli and Pavel Pevzner. Transforming Cabbage into Turnip. Proceedings of the 27th Annual Symposium on Theory of Computing (STOC95), pages 178–189, 1995.
[Sie01] Adam C. Siepel. Exact Algorithms for the Reversal Median Problem. Master's thesis, University of New Mexico, December 2001.
[Sie02] Adam C. Siepel. An Algorithm to Enumerate All Sorting Reversals. RECOMB, pages 281–290, April 2002.
Comments
bruh