As punishment for being naughty, Dante has been trapped in a strange house with many rooms. The house is an ~N \times N~ grid of rooms, with ~N~ odd and greater than ~1~. The upper left room is numbered ~1~, and then the other rooms are numbered ~2, 3, \dots, N^2~, in a clockwise spiral pattern. That is, the numbering proceeds along the top row of the grid and then makes a 90 degree turn to the right whenever a grid boundary or an already numbered room is encountered, and finishes in the central room of the grid. Because ~N~ is odd, there is always a room in the exact center of the house, and it is always numbered ~N^2~.

For example, here are the room numberings for houses with ~N = 3~ and ~N = 5~:

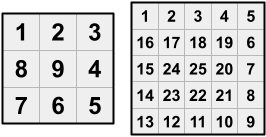
Dante starts off in room ~1~ and is trying to reach the central room (room ~N^2~). Throughout his journey, he can only make moves from his current room to higher-numbered, adjacent rooms. (Two rooms must share an edge — not just a corner — to be adjacent.)

Dante knows that he could walk from room to room in consecutive numerical order — i.e., if he is currently in room ~x~, he would move to room ~x+1~, and so on. This would take him exactly ~N^2-1~ moves. But Dante wants to do things his way! Specifically, he wants to reach the central room in exactly ~K~ moves, for some ~K~ strictly less than ~N^2-1~.

Dante can accomplish this by taking one or more shortcuts. A shortcut is a move between rooms that are not consecutively numbered.

For example, in the ~5 \times 5~ house above,

• If Dante is at ~1~, he cannot move to ~17~, but he can move to ~2~ or to ~16~. The move to ~2~ is not a shortcut, since ~1+1 = 2~. The move to ~16~ is a shortcut, since ~1+1 \ne 16~.
• From ~2~, it is possible to move to ~3~ (not a shortcut) or to ~17~ (a shortcut), but not to ~1~, ~16~, or ~18~.
• From ~24~, Dante can only move to ~25~ (not a shortcut).
• It is not possible to move out of room ~25~.

As a specific example using the ~5 \times 5~ house above, suppose that ~K = 4~. One option is for Dante to move from ~1~ to ~2~, then move from ~2~ to ~17~ (which is a shortcut), then move from ~17~ to ~18~, then move from ~18~ to ~25~ (which is another shortcut). This is illustrated below (the red arrows represent shortcuts):

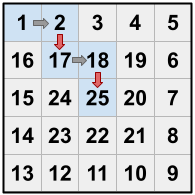
Can you help Dante find a sequence of exactly ~K~ moves that gets him to the central room, or tell him that it is impossible?

Input Specification

The first line of the input gives the number of test cases, ~T~. ~T~ test cases follow. Each test case consists of one line with two integers ~N~ and ~K~, where ~N~ is the dimension of the house (i.e. the number of rows of rooms, which is the same as the number of columns of rooms), and ~K~ is the exact number of moves that Dante wants to make while traveling from room ~1~ to room ~N^2~.

Output Specification

For each test case, output one line containing Case #x: y, where ~x~ is the test case number (starting from ~1~).

If no valid sequence of exactly ~K~ moves will get Dante to the central room, ~y~ must be IMPOSSIBLE.

Otherwise, ~y~ must be an integer: the number of times that Dante takes a shortcut, as described above. (Notice that because Dante wants to finish in strictly less than ~N^2-1~ moves, he must always use at least one shortcut.) Then, output ~y~ more lines of two integers each. The ~i^\text{th}~ of these lines represents the ~i^\text{th}~ time in Dante's journey that he takes a shortcut, i.e., he moves from some room ~a_i~ to another room ~b_i~ such that ~a_i+1 < b_i~.

Notice that because these lines follow the order of the journey, ~a_i < a_{i+1}~ for all ~1 \le i < y~.

Limits

~1 \le T \le 100~.

~1 \le K < N^2-1~.

~N \bmod 2 \equiv 1~. (~N~ is odd.)

Test Set 1

Time limit: 5 seconds.

~3 \le N \le 9~.

Test Set 2

Time limit: 20 seconds.

~3 \le N \le 39~.

Test Set 3

Time limit: 20 seconds.

~3 \le N \le 9999~.

Sample Input

4
5 4
5 3
5 12
3 1

Sample Output

Case #1: 2
2 17
18 25
Case #2: IMPOSSIBLE
Case #3: 2
11 22
22 25
Case #4: IMPOSSIBLE

Sample Case #1 is described in the problem statement. Dante's route is ~1 \to 2 \to 17 \to 18 \to 25~. Because ~1 \to 2~ and ~17 \to 18~ are moves between consecutively numbered rooms, they are not included in the output. Only the shortcuts (~2 \to 17~ and ~18 \to 25~) are included.

In Sample Case #2, there is no solution. (Recall that there is no way for Dante to move diagonally.)

In Sample Case #3, observe that ~22~ appears both as the end of one shortcut and the start of the next. It would not be valid to include the line 11 22 25 in the output; each line must represent a single shortcut.

The image shows a ~5 \times 5~ grid of rooms numbered as described in the statement. A path with arrows is shown as described above. The arrows between ~11~ and ~22~ as well as ~22~ and ~25~ are red to show they are shortcuts.

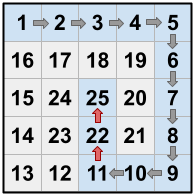
There is another solution that uses only one shortcut: Dante can move from ~1 \to 2 \to 3 \to 4 \to 5 \to 6~, then move from ~6 \to 19~ (a shortcut), then move from ~19 \to 20 \to 21 \to 22 \to 23 \to 24 \to 25~. This is also valid; there is no requirement to minimize (or maximize) the number of shortcuts taken.

In Sample Case #4, Dante cannot get to the central room (~9~, in this case) in just one move.

Note

This problem has different time limits for different batches. If you exceed the Time Limit for any batch, the judge will incorrectly display >20.000s regardless of the actual time taken. Refer to the Limits section for batch-specific time limits.