You are given an infinite chessboard. In this task, a chessboard is an infinite two-dimensional grid of squares, where each square is indexed by a pair of integers ~(r,c)~, denoting the row and the column respectively. The only piece currently present on the chessboard is the superpiece. You are given a list of valid moves of your superpiece, which will be specified as a non-empty string containing a subset of the characters in QRBNKP. In each turn, the superpiece can move as one of the given chess pieces. The superpiece is initially positioned at square ~(a,b)~. Calculate the minimum number of moves needed to reach the square ~(c, d)~.

The subset of the chess rules applicable for this problem are given below. There are six types of pieces: queen, rook, bishop, knight, king and pawn. They move the following way:

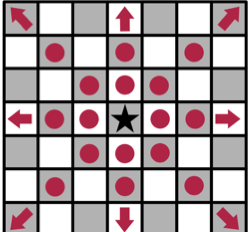
• The Queen (denoted by Q) can move to any square in the same row, column or diagonal as the square it is currently in. Formally, for any integer ~k \neq 0~, a queen can move from ~(a, b)~ to ~(a, b + k)~, ~(a + k, b)~, ~(a + k, b + k)~ and ~(a + k, b - k)~.

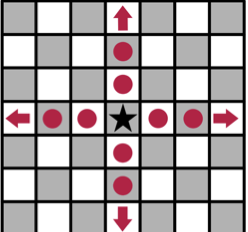
• The Rook (denoted by R) can move to any square in the same row or in the same column as the square it is currently in. Formally, for any integer ~k \neq 0~, a rook can move from ~(a, b)~ to ~(a + k, b)~ and ~(a, b + k)~.

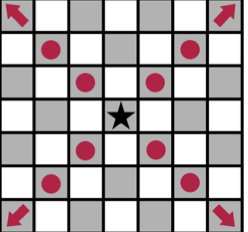
• The Bishop (denoted by B) can move to any square in the same diagonal as the square it is currently in. Formally, for any integer ~k \neq 0~, a bishop can move from ~(a, b)~ to ~(a + k, b + k)~, and ~(a + k, b - k)~.

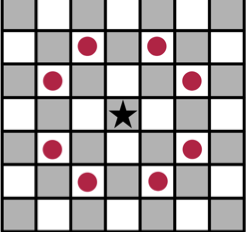
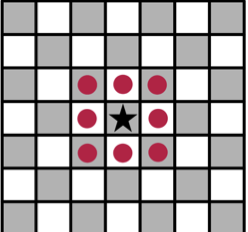
• The kNight (denoted by N) can move in the shape of an 'L': that is, it first moves two squares in a particular direction followed by a move of one sqaure in an perpendicular direction. Formally, a knight can move from ~(a,b)~ to ~(a+1,b+2)~, ~(a+1,b-2)~, ~(a + 2, b + 1)~, ~(a + 2, b - 1)~, ~(a - 2, b + 1)~, ~(a - 2, b - 1)~, ~(a - 1, b + 2)~, and ~(a - 1, b - 2)~.

• The King (denoted by 'K') can move to any of the eight squares directly adjacent to the current square. Formally, a king can move from ~(a,b)~ to ~(a,b+1)~, ~(a,b-1)~, ~(a+1,b)~, ~(a-1, b)~, ~(a + 1, b + 1)~, ~(a + 1, b - 1)~, ~(a - 1, b + 1)~ and ~(a - 1, b - 1)~.

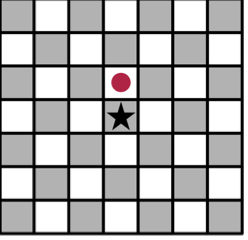
• The Pawn (denoted by 'P') can move exactly one square up. Formally, a pawn can move from ~(a, b)~ to ~(a + 1, b)~.

Note that the other rules or moves that you might know about chess do not apply in this problem; please only use the ones listed above.

Also, note that while the symbol denoting the chess piece is often the first letter of its name in English, it is the second letter for the "kNight" (to avoid confusion with the "King").

Input Specification

The first line of the input contains an integer ~q~, representing the number of queries your program will be tested on. Each two of the following lines describe a query:

The first line of a query contains a non-empty string specifying the set of chess pieces the superpiece can move as. This string contains a subset of the characters in the uppercase string "QRBNKP", with the contained characters appearing in the same order. In other words, it is in the form of a sub-sequence of "QRBNKP".

The second line of a query contains four space-separated integers ~a, b, c, d~ - the original and the target position of the superpiece. It is guaranteed that ~(a, b) \neq (c, d)~, that is, the original position is different from the target.

Output Specification

For each of the ~q~ queries, output a single line containing an integer ~m~ representing the minimum number of moves the superpiece needs to reach the target from its original position for that query. If it is not possible to reach the target from the original position for a query, output -1 instead.

Constraints

~1 \leq q \leq 1000~, ~- 10^8 \leq a,b,c,d \leq 10^8~ for each query. The chess board is infinite in all directions.

Scoring

• Subtask 1 (12 points): No N character and a guaranteed Q character in the first line of each query.
• Subtask 2 (9 points): Guaranteed Q and N characters (both) in the first line of each query.
• Subtask 3 (13 points): No Q character and a guaranteed R character in the first line of each query.
• Subtask 4 (8 points): The first line of each query is always B.
• Subtask 5 (6 points): No Q or R characters and a guaranteed B character in the first line of each query.
• Subtask 6 (31 points): The first line of each query is always N.
• Subtask 7 (8 points): No Q, R, or B characters and a guaranteed N character in the first line of each query.
• Subtask 8 (7 points): No Q, R, B, or N characters and a guaranteed K character in the first line of each query.
• Subtask 9 (6 points): The first line of each query is always P.
• Note that subtasks are not ordered in the expected order of their difficulty.

Sample Input 1

2
NKP
3 3 5 1
NKP
2 6 5 3

Sample Output 1

2
2

Explanation

In the first query, we are asked to go from ~(3,3)~ to ~(5,1)~, using the moves of knight, king and pawn. There are multiple ways of doing this in exactly 2 moves, for example:

• Move as a pawn to ~(4, 3)~, then as a knight to ~(5, 1)~.
• Move as a knight to ~(5, 2)~, then as a king to ~(5, 1)~.
• Move as a king to ~(4, 2)~, and then again as a king to ~(5, 1)~.

There is no way of achieving this by fewer than two moves - we would need a bishop or a queen to do that.

In the second query, we are asked to go from ~(2, 6)~ to ~(5, 3)~. Again, the optimal solution is to use two moves. This time, both of these moves have to be knight moves, with the intermediate square being ~(4, 5)~ or ~(3, 4)~.

Sample Input 2

2
B
2 8 3 6
B
2 8 5 5

Sample Output 2

-1
1

Explanation

In the first query, we are asked to go from ~(2, 8)~ to ~(3, 6)~. Provided only the bishop's moves, it is not possible to do this.

In the second query, we are asked to go from ~(2, 8)~ to ~(5, 5)~, again using only bishop's moves. It is possible to do this in one move.

Sample Input 3

2
Q
3 3 4 5
QR
4 1 1 4

Sample Output 3

2
1

Explanation

In the first query, we are asked to go from ~(3, 3)~ to ~(4, 5)~ using the queen's moves. It is possible to do this in two moves, for instance, by using ~(4, 4)~ as an intermediate point.

In the second query, we are asked to go from ~(4, 1)~ to ~(1, 4)~, using the moves of queen and rook. It is possible to do this in one move.