There are two kinds of lego bricks, characterized by their dimensions: $1\times 1\times 1$ and $2\times 1\times 1$ (width, height and depth, respectively, as shown below). You have an infinite supply of each of them, and within each kind, they are indistinguishable.

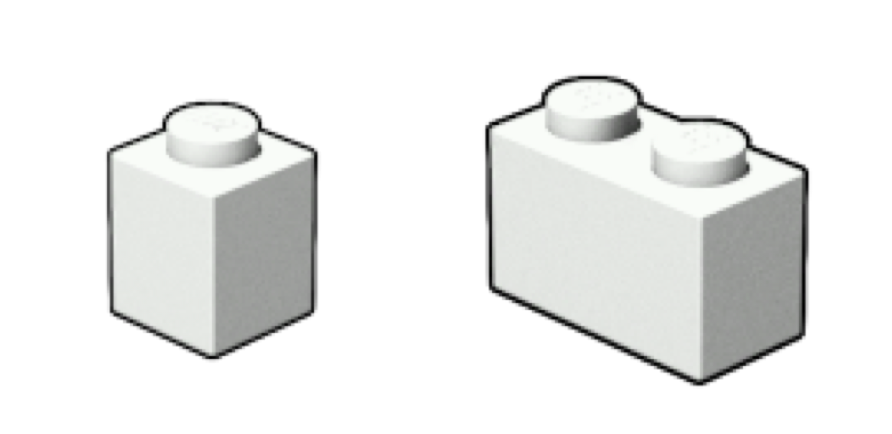
A lego brick is always used in upright position. The faces on the sides are made from identical material and are indistinguishable, except their dimensions.

We consider two lego bricks to be locked if one is directly above the other. Two bricks $b_0$ and $b_k$ are said to be connected if there is a sequence of bricks $b_0,b_1,\dots ,b_k$ such that bricks $b_{i-1}$ and $b_i$ are locked for all $i$ such that $1\le i\le k$. We consider an arrangement of bricks connected if each pair of bricks within this arrangement is connected.

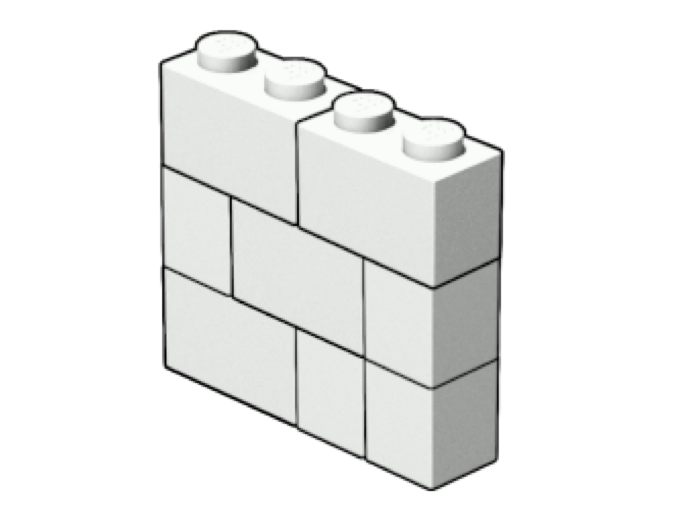
You would like to build a thin rectangular wall with width $w$ and height $h$ (and depth 1) such that the wall contains no holes and its brick arrangement is connected. As an example, below is a such a lego wall of width 4 and height 3:

On the other hand, the following $4\times 3$ lego wall is not connected, and therefore is not desired:

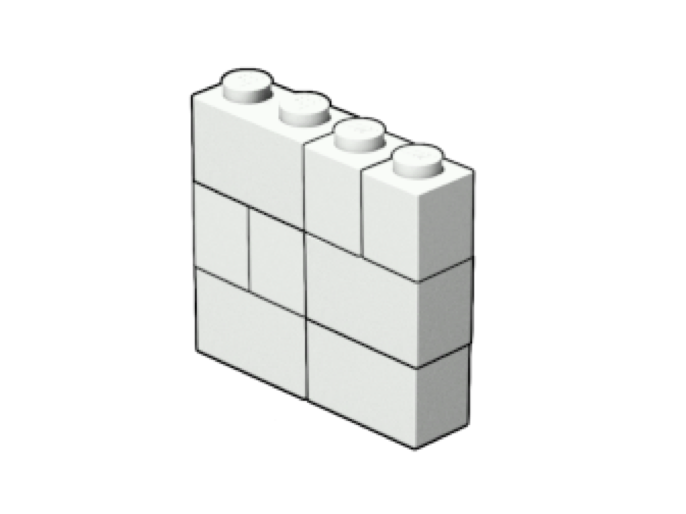
How many ways of building a connected wall with no holes are there? Since this number may be large, output it modulo $1000000007$.

Note that the mirrored (180-degree rotated) version of a lego wall is considered to be a different wall, unless the mirrored wall looks identical to the original wall.

Input Specification

The input consists of a single line containing two space separated integers $w$ and $h$ ($1\le w\le 250000,2\le h\le 250000,w\times h\le 500000$) – the width and the height of the wall, respectively.

Output Specification

Output a single integer – the number of hole-free connected lego walls of dimensions $w\times h$, modulo $1000000007$.

Sample Input 1

2 2

Sample Output 1

3

Sample Input 2

3 3

Sample Output 2

12

Sample Input 3

5 7

Sample Output 3

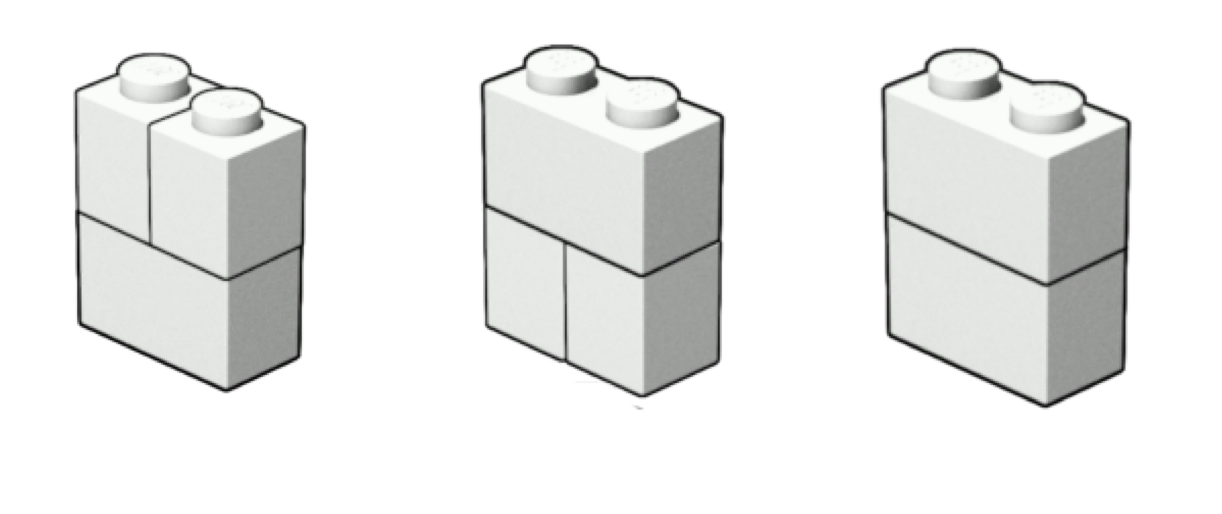
1436232

Explanation for Sample Input 1

The three connected $2\times 2$ walls one can build are:

Constraints

• Subtask 1 (14 points): $w=2$.
• Subtask 2 (12 points): $h=2$.
• Subtask 3 (18 points): $w,h\le 100$.
• Subtask 4 (30 points): $w\le 700$.
• Subtask 5 (20 points): $h\le 700$.
• Subtask 6 (6 points): no additional constraints.