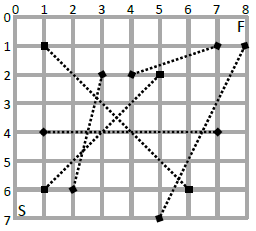
The cities of the future will be laid out in perfect grids. Nobody will drive or take the bus. Transit problems will have been solved once and for all by placing teleportation devices (TDs) at intersections. Pedestrians entering an intersection containing a TD will have the option of continuing through the intersection as normal or using an app on their phone to trigger the TD and instantly teleport themselves to a new intersection. The TDs will be linked in pairs as shown below. Either TD in the pair can be used to instantly teleport a pedestrian to the other TD.

Intersections are identified using a pair of integers representing the horizontal street number (numbered North to South starting at $0$) and then the vertical street number (numbered West to East starting at $0$).

Suppose a future pedestrian wants to go from the point marked $S$ $(7,0)$ to the point marked $F$ $(0,8)$ on the map shown to the right. She could use the TD at $(6,1)$ to instantly teleport to $(2,5)$. If she does that, her total distance will be $7$ blocks: she walks $2$ blocks from $S$ to $(6,1)$ then $5$ from $(2,5)$ to $F$. If she takes the TD at $(7,5)$, she can shorten her route to $6$ blocks. But there is also a combination of $2$ TDs that can get her to $F$ in $5$ blocks. Can you find it?

The input will contain $10$ test cases. The first line of each test case consists of a pair of numbers $H$ and $V$ which give the number of horizontal and vertical streets in a future city $(1\le H,V\le 1000)$. This is followed by a line with two integers $S_h$ and $S_v$ representing the start location of a pedestrian and another line with two integers $F_h$ and $F_v$ representing their finishing location $(0\le S_h,S_v,F_h,F_v\le 999)$. This is followed by a line with a single integer $N$ which gives the number of pairs of TDs $(0\le N\le \frac{HV}{4})$ and this is followed by $N$ lines, each containing four integers $T_h$, $T_v$, $U_h$ and $U_v$ representing the locations of the two TDs in each pair. Each intersection can hold only one TD.

Your job is to find the shortest path between the pedestrian's start and finish locations and report the number of city blocks the pedestrian will have to walk. The path can make use of any number of teleportation devices.

Note that the data set below contains only $3$ test cases, but the real data set will contain $10$.

Sample Input

8 9
7 0
0 8
6
1 1 6 6
4 1 4 7
6 1 2 5
2 3 6 2
1 8 7 5
2 4 1 7
5 4
4 0
0 3
2
2 1 0 3
4 1 2 2
1000 1000
5 2
10 970
14
0 3 4 5
1 1 13 13
1 2 2 3
7 7 9 9
1 70 70 1
9 1 1 12
2 2 3 3
3 7 2 900
3 900 5 95
3 90 5 100
4 5 5 4
6 7 8 9
9 9 8 8
9 9 5 3

Sample Output

5
2
83

Educational Computing Organization of Ontario - statements, test data and other materials can be found at ecoocs.org