ICPC East Central NA Regional Contest 2016, Problem G

Roberta Roberts (the older sister of Bobby in Problem F) teaches math at a small college, and has just introduced the Tower of Hanoi to the students in her Discrete Math class. In case you've been in a Tibetan monastery for the past several years and have never heard of the Tower of Hanoi puzzle (doubtful for several reasons), here's a brief description. The puzzle consists of three pegs, and $n$ disks with radii of $1,2,\dots ,n$. The initial setup has all the disks on a start peg in increasing order of their size from top to bottom, forming a pyramid. The object of the puzzle is to move all of these disks to a destination peg using the following rules:

1. You can move only one disk at a time
2. At no point may a larger disk lie on top of a smaller disk

It's well known that the optimal (i.e., shortest) solution for a Tower of Hanoi puzzle with $n$ disks involves $2^n-1$ moves. The optimal solution for $n=3$ is shown below (where the start peg is the leftmost peg and the destination peg is the rightmost peg):

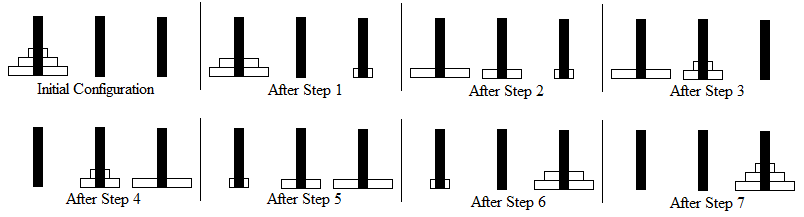
As part of an in-class lab, Roberta will hand out Tower of Hanoi sets to her students and let them try to solve the problem on their own. As she goes around the room, she realizes that for the larger size sets, she has trouble looking at a current layout of the disks and determining whether the student is on the right track or not. In other words, she wishes to know whether or not a given configuration of the puzzle is one of the $2^n$ configurations in the optimal solution sequence. She would also like to be able to tell her students how close they are to the final configuration (i.e., all the disks in increasing sizes, top to bottom, on the destination peg). Needless to say, this has caused her a bit of consternation, so she has come to you for help.

Input Specification

Input consists of three lines, each line representing one peg of a Tower of Hanoi configuration. Each of these lines starts with a non-negative integer $m$ indicating the number of disks on that peg, followed by $m$ integers indicating the disks, starting with the disk on the bottom of the peg. The first line refers to the start peg and the last line refers to the destination peg. Disks are numbered consecutively starting at $1$ with each number indicating the disk's radius. All disk numbers used form a consecutive sequence. The maximum number of disks in any test case is $50$.

Output Specification

Display No if the given configuration is not in the optimal solution sequence; otherwise display the minimum number of remaining moves required to get to the final configuration.

Sample Input 1

1 3
2 2 1
0

Sample Output 1

4

Sample Input 2

1 3
0
2 2 1

Sample Output 2

No