Consider an empty diagram of $N$ points, where $N$ is an even number. You can compute the number of ways to complete this using dynamic programming in $\mathcal{O}(N^2)$ or $\mathcal{O}(N)$. The sequence formed is the Catalan number sequence.

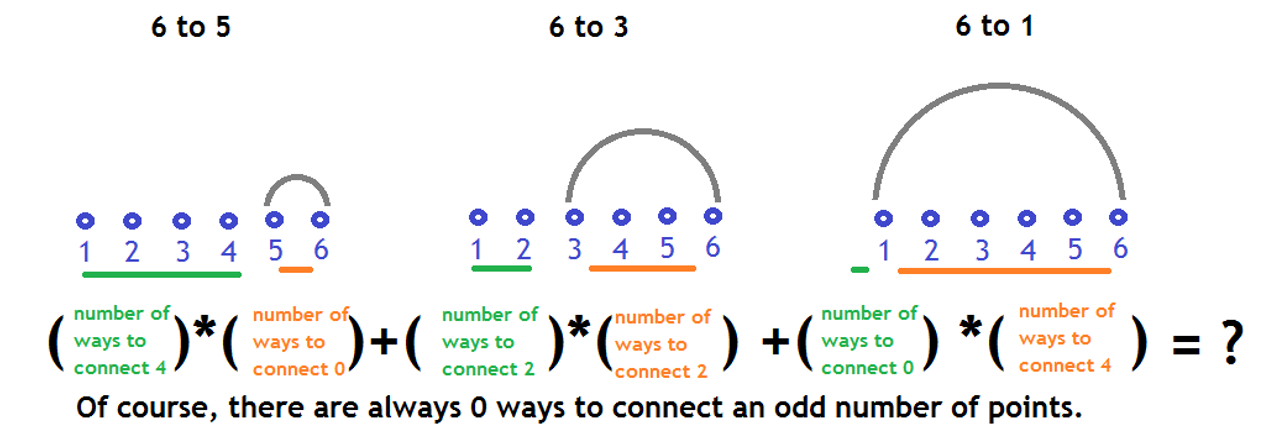
Now, it should be possible to look up the number of ways to connect any group of $n$ dots, as long as $n$ is less than $N$. From this point, we will refer to looking up the number of ways to connect a value $n$ as $C(n)$. Notice that, given an empty sequence of $Q$ dots, you can remove any subset of exactly $P$ dots and there will always be the same number of ways to complete the diagram.

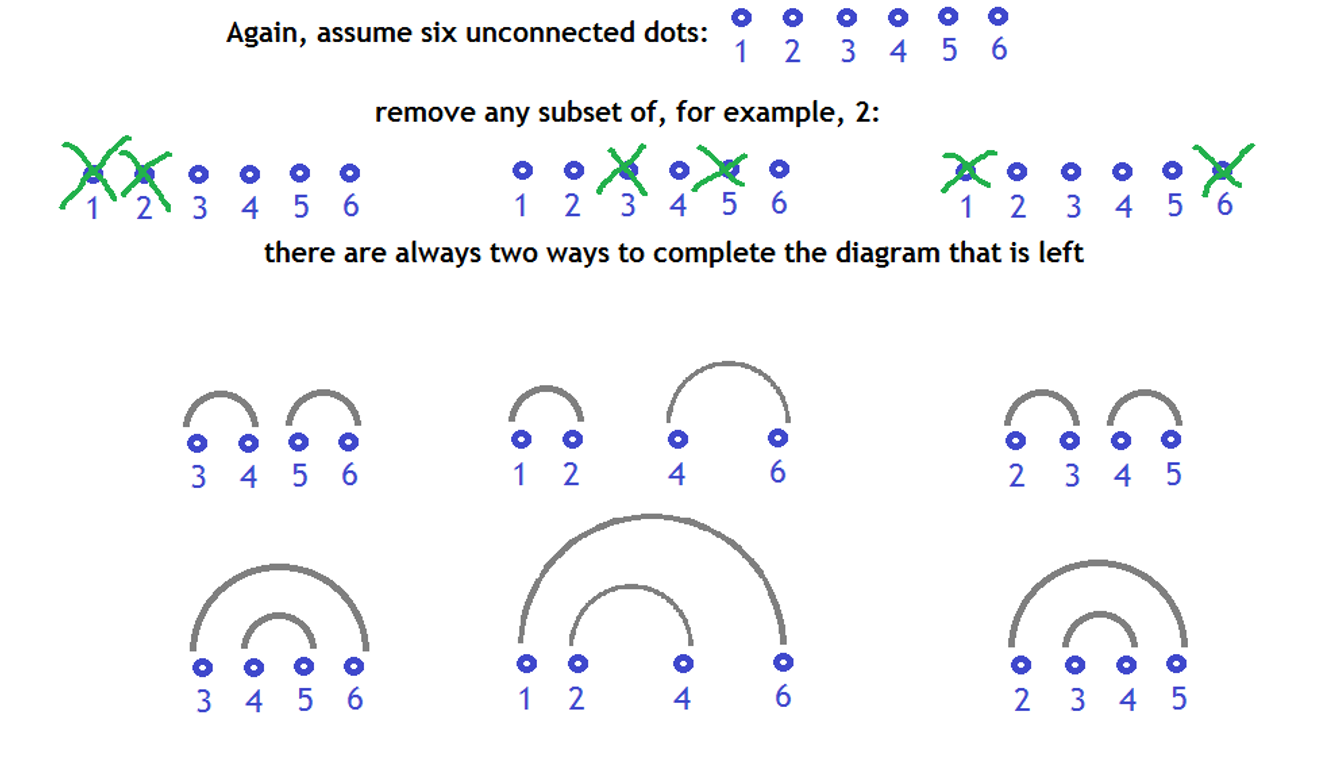
We can take this observation a step further by noticing that if there are multiple semicircles within a larger semicircle, and multiple possible combinations all happen to cover up the same number of dots from that semicircle, then the number of ways to complete that portion of the diagram with a known number of dots excluded is constant and can be looked up as a function of $C$. Just remember that this doesn't work unless all dots contained within the smaller circles have already been considered.

Therefore, for each circle initially drawn in red, find the number of ways different to pair up all quantities of dots from zero to the diameter of the semicircle using the dots contained within it, without erasing this semicircle. For each circle, you can't start finding combinations until the contained circles have already been considered. It might also help to assume that all dots are always covered up by one huge semicircle, and the goal of the program is to find the number of ways to complete the part of the diagram under that semicircle (all of it) without erasing it.

There's one more step, which is to consider for each semicircle in red what would happen if we do not erase this circle. Obviously, we must compute the number of ways to connect all points underneath. Take the stored numbers for this circle discussed earlier, and for every $E$ ways to completely connect $I$ dots, map it to $C(W-2-I)\ast E$, where $W$ is the width of the semicircle. Sum it all up. The proof is left as an exercise to the reader.

A final note: building the data structure to store the number of ways to completely connect $I$ dots for all $I$ up to $N$ is not complex, but a naïve way ($\mathcal{O}(N^N)$ per semicircle) will be insufficient. There is a way to compute combinations which seems like it is $\mathcal{O}(N^3)$ per semicircle, but keep in mind that no two semicircles intersect. This makes the mentioned way $\mathcal{O}(N^2)$ per semicircle, of which there are $K$ in total. Finding this way to create combinations will again be left up to the reader.

Final time complexity: $\mathcal{O}((K+N)\ast N)$