COI '19 #2 Pastiri
View as PDF"I never felt so full that I couldn't eat one more lamb." – Mr. Malnar
A flock of sheep lives in a tree, a simple connected graph without a cycle. The tree contains
nodes
denoted with integers from
to
. Each node of a tree is a home to at most one sheep. A wise shepherd
realized that, sooner or later, wolves will learn how to climb trees.
In order to protect the sheep, we need to place shepherds into some nodes such that each sheep is protected by at least one shepherd. It is known that each shepherd protects all sheep that are closest to him, and only them. The distance between some sheep and some shepherd is equal to the number of nodes on a unique path between the node containing the sheep and the node containing the shepherd (inclusive). Additionally, the shepherd can share a node with a sheep. Of course, in that case he protects only that sheep.
Determine the minimal number of shepherds that need to be placed in the nodes of a tree such that each sheep is protected by at least one shepherd. Additionally, determine one such arrangement of shepherds.
Input Specification
The first line contains integers and
from the task description.
Each of the next lines contains two integers
and
which indicate that there is an undirected edge between nodes
and
.
The next line contains different integers
that represent nodes which contain a sheep.
Output Specification
In the first line, you should output a number which represents the minimal number of shepherds from
the task description.
In the second line, you should output space-separated integers which represent the nodes containing
shepherds.
If there are multiple correct solutions, you may output any of them.
Constraints
| Subtask | Points | Constraints |
|---|---|---|
| 1 | 8 | |
| 2 | 18 | |
| 3 | 23 | |
| 4 | 51 |
Sample Input 1
4 2
1 2
2 3
3 4
1 4Sample Output 1
2
1 3Sample Input 2
9 5
1 2
2 3
3 4
3 5
1 6
1 7
7 8
8 9
2 5 6 7 9Sample Output 2
3
1 4 9Sample Input 3
20 9
1 2
2 3
2 4
4 5
4 6
5 7
7 8
8 9
7 10
10 11
6 12
6 13
6 17
13 14
14 15
14 16
17 18
18 19
18 20
1 3 9 11 12 15 16 19 20Sample Output 3
3
5 14 18Explanation for Sample Output 3
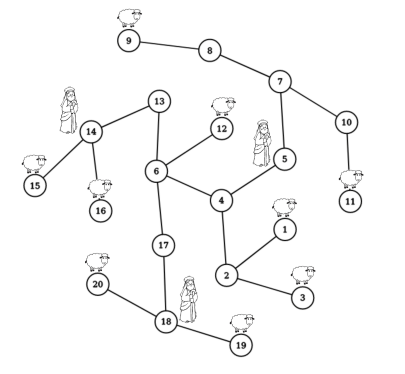
Comments