Mirko recently read about Pick's theorem that says the following: in the coordinate system, if we draw a polygon whose vertices are points with integer coordinates, and if $A$ denotes its area, $i$ the number of points with integer coordinates located inside the polygon, and $b$ the number of points with integer coordinates located on its edges (including the polygon's vertices), then it always holds:

$${\displaystyle A=i+\frac{b}{2}-1}$$

In order to test the theorem, Mirko used his smartboard to create a polygon from magnetic sticks that have, during the night, sunk to the bottom of the board because due to gravity. Now, Mirko wants to construct a polygon of the minimal possible area while using all the sticks he found. Mirko can move the sticks anywhere on his board, but he must not rotate them. Mirko is equipped with the following:

• a horizontal sticks of length $1$,
• b vertical sticks of length $1$,
• c diagonal sticks of length $\sqrt{2}$ that form a ${45}^{\circ }$ angle with the positive part of $x$-axis,
• d diagonal sticks of length $\sqrt{2}$ that form a ${135}^{\circ }$ angle with the positive part of $x$-axis.

Figure 2: For the polygon above: $A=8$, $i=4$, $b=10$.

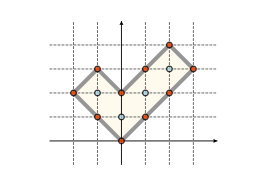
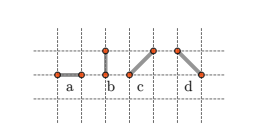
Determine the polygon of the minimal possible area that can be obtained so that all the sticks are used. You can assume that the input data is such that it is possible to construct at least one such polygon.

Also, it is possible to score partial points if, using all of the given sticks, you construct a valid polygon (that is not necessarily of the minimal possible area).

Input Specification

The first line of input contains four integers $a,b,c,d$ from the task.

Output Specification

You must output $n$ lines where $n=a+b+c+d$. In the $j^{\text{th}}$ line, output integers $x_j$ and $y_j$ — the coordinates of the $j^{\text{th}}$ polygon vertex. The first polygon vertex must be $(0,0)$, and the other vertices can be printed in an arbitrary direction (either positive or negative). It is allowed that the consecutive polygon sides are parallel, but the polygon cannot touch or intersect itself.

Constraints

For all subtasks:

$0\le a,b,c,d\le 100$

$a+b+c+d\ge 3$

Subtask	Points	Constraints
1	5	$c=d=0$
2	5	$a=b=0$
3	10	$a+b+c+d\le 6$
4	10	$a+b+c+d\le 20$
5	10	$a+b+c+d\le 40$
6	10	$a+b+c+d\le 80$
7	10	$a+b+c+d\le 150$
8	10	$a+b+c+d\le 200$
9	10	$a+b+c+d\le 300$
10	20	No additional constraints.

If, for a test case, your solution does not output a valid polygon that consists of the given sticks, then it scores $0$ points for the corresponding subtask. If the solution outputs a valid polygon that is not of the minimal possible area, then it can score partial points according to the following rules.

For test case $j$, let $r_j$ denote the ratio of area of the obtained polygon and the minimal possible polygon area. For subtask $k$, let's denote with $z_k$ the largest of the numbers $r_j$, where $j$ is the test case from subtask $k$. The percentage of points $P_k$ that the solution scores for subtask $k$ depends on the number $z_k$ in the following way: $P_k=10$ if $z_k\ge 3$, and otherwise it is calculated as:

$${\displaystyle P_k=\frac{25}{8}(3-z_k{)}^4+10}$$

Therefore, a solution that is not optimal can score between $10\mathrm{\%}$ and $60\mathrm{\%}$ points for a certain subtask, depending on the ratio of the area of the obtained polygon and the optimal one.

Sample Input 1

1 1 1 0

Sample Output 1

0 0
1 1
0 1

Sample Input 2

0 0 6 4

Sample Output 2

0 0
1 1
2 2
3 3
2 4
1 3
0 2
-1 3
-2 2
-1 1