For the first subtask, the number of points within the convex hull of any subset of points is equal to the size of that subset, so the expected value is ~\frac{n}{2}~ and ~m = 2^{n-1}n~.

We can calculate ~m~ by going over each of the ~2^n~ subsets of points, finding the convex hull and checking to see how many points lie in the hull. A naive implementation of this was sufficient to solve the subtask in which ~n \le 15~.

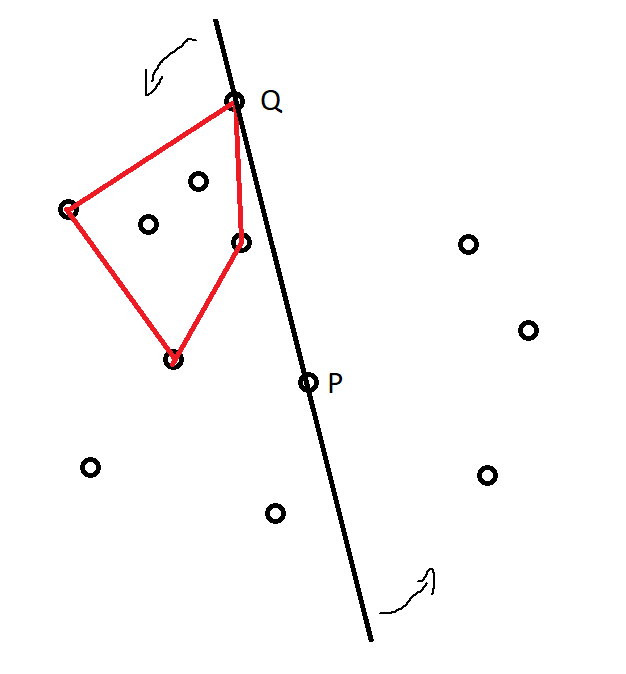
We can also calculate ~m~ in a different way - by fixing a point and counting how many subsets there are where the point lies in the hull. It turns out that it's easier to count the complement, i.e. how many subsets there are whose hull doesn't contain the fixed point. Notice that after fixing a point and a subset whose hull doesn't contain it, there is always a line that passes through the point, but which doesn't intersect the hull. If we call the fixed point ~P~, we can think of this line as rotating around ~P~ counterclockwise until it hits a point ~Q~ on the hull (see image above).

For a fixed choice of ~P~ and ~Q~ it is sufficient to find the number of points which lie on one side of the line ~PQ~. If we call this number ~k~ (not counting ~Q~), then the number of subsets whose hull doesn't contain ~P~ and for which ~Q~ is the point that is 'first in the counterclockwise direction' is ~2^k~.

Therefore, the solution can be determined in the following way. Fix a point ~P~ and sort the remaining points circularly around ~P~. Iterate over ~Q~ and maintain the number of points on each side of the line ~PQ~. The points in a halfplane form a circular segment, so it is enough to maintain the last point (with respect to the circular order) that is still in the current halfplane, using the method of two pointers. For each point ~P~ we do one sort in ~\mathcal O(n \log n)~ and then calculate the number of subsets not containing ~P~ in ~\mathcal O(n)~ with two pointers. The total complexity is then ~\mathcal O(n^2 \log n)~.

For the circular sort and for maintaining the current halfplane it is helpful to use the function ~\text{CCW}(A, B, C)~ which determines for three given points ~A~, ~B~ and ~C~ whether they are listed in counterclockwise order:

$$\displaystyle \text{CCW}(A, B, C) = x_A(y_B-y_C) + x_B(y_C-y_A) + x_C(y_A-y_B)$$

where ~\text{CCW}(A, B, C) > 0~ if and only if the points ~A~, ~B~ and ~C~ are listed in counterclockwise order. To sort the points circularly, we can divide them into the ones above and the ones below point ~P~, sort these two groups separately, and then merge them. Within a group we use the ~\text{CCW}~ function as a comparator with arguments being the two points in question and the fixed point ~P~.