Five in the morning. Daniel wakes up, he opens his eyes. His head hurts a bit. He can still hear the ringing in his ears.

He comes to realize that he has found himself at a playground, in a big metal box.

He remembers a similar situation he found himself in, three years ago, COCI round 2, task Kocka.

But this time, things are much more complicated... Daniel is in an ~n~-dimensional hypercube ~\mathcal Q_n~. ~2^{n-1}~ identical copies of a tree ~\mathcal T~ with ~n~ edges are scattered around him. It soon became clear to him that salvation lies in tiling the edges of the hypercube with the trees.

Formally, a hypercube ~\mathcal Q_n~ is a graph with nodes ~0, 1, \dots, 2^n-1~, in which nodes ~x~ and ~y~ are connected if and only if their bitwise xor is a power of two.

A tree can be placed on the hypercube so that:

• each node of the tree corresponds to some node of the hypercube
• those nodes have to be distinct
• if there is an edge between two nodes in the tree, then there has to be an edge between the corresponding nodes in the hypercube.

A tiling of the hypercube is done by placing several trees so that each edge of the hypercube belongs to at most one tree.

Your task is to tile the hypercube ~\mathcal Q_n~ with as many copies of the given tree ~\mathcal T~, which has ~n~ edges.

Input Specification

The first line contains a positive integer ~n~ ~(1 \le n \le 16)~, the dimension of the hypercube.

Each of the following ~n~ lines contains two integers ~x~ and ~y~ ~(0 \le x, y \le n, x \neq y)~ which denote that the nodes ~x~ and ~y~ are connected by an edge in tree ~\mathcal T~.

Output Specification

In the first line print the number of trees in your tiling.

Each of the following lines should describe a placement of a single copy of the tree ~\mathcal T~.

In the ~i^\text{th}~ line print ~n+1~ numbers ~a_0^{(i)}, a_1^{(i)}, \dots, a_n^{(i)}~. These numbers denote that the ~i^\text{th}~ tree is placed so that the hypercube node ~a_j^{(i)}~ corresponds to the tree node ~j~, for all ~j = 0, \dots, n~.

Scoring

If your solution correctly places ~k~ trees, you will receive ~f(k) \cdot 110~ points for that test case, where

$$\displaystyle f(k) = \begin{cases} 0.7 \cdot k/2^{n-1} & \text{if }k < 2^{n-1} \\ 1 & \text{if }k = 2^{n-1} \end{cases}$$

Of course, if your solution is not correct, you will receive ~0~ points.

Your total number of points is equal to the minimum number of points your solution receives over all of the test cases.

It is possible to prove that there always exists a solution which uses all of the ~2^{n-1}~ trees.

Sample Input 1

1
0 1

Sample Output 1

1
0 1

Sample Input 2

2
0 1
1 2

Sample Output 2

2
0 1 3
0 2 3

Sample Input 3

3
0 1
0 2
0 3

Sample Output 3

4
0 1 2 4
3 1 2 7
5 1 4 7
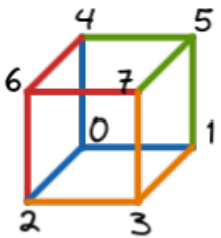
6 2 4 7

Explanation for Sample Output 3