Notice that for each valley, there is a segment of ~x~-coordinates for which a fairy illuminates this valley.

In the first subtask, the segments are determined by the points adjacent to the valley. We can just intersect the lines with the line ~y = h~. The complexity of this step is ~\mathcal O(n)~.

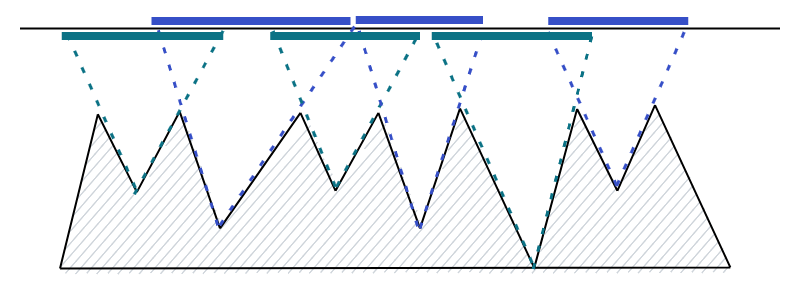
After we find the segments, we have the well-known problem of covering a set of segments with the minimum number of points. The greedy algorithm where we sort the segments by their right end is correct, and the complexity is ~\mathcal O(n \log n)~.

When the mountain tops have different heights, there is an issue: it can happen that a nonadjacent mountain top "blocks the view":

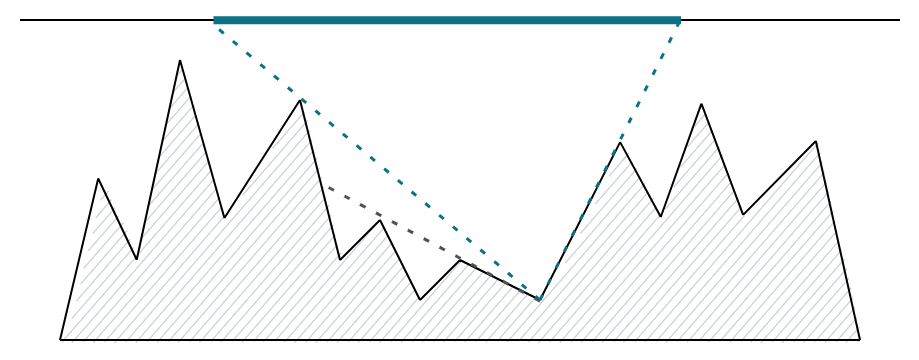
For the second subtask, we can look at each valley-mountain top line, and determine the segment from the intersections of the lines with the line ~y = h~. The complexity is ~\mathcal O(n^2)~.

For the full solution, note that the mountain top which "blocks the view" is actually the penultimate point on the upper convex hull of all the points up to the current valley:

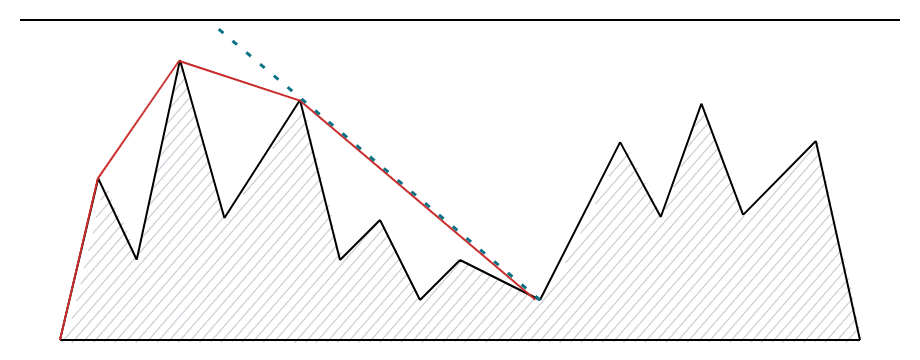
Hence, maintaining the convex hull is enough to find the left ends of all the segments. We can do the same thing (but backwards) for the right ends. The complexity of this part is ~\mathcal O(n)~.