The first subtask can be solved in multiple ways. We will describe the solution using hashing which will be useful for the final subtask. Let's root the tree in a node ~R~. We are interested in all palindromic segments with one end in node ~R~. For every node ~X~, we will calculate two values:

$$\displaystyle \begin{align*} down_x &= x_0 B^{k-1} + x_1 B^{k-2} + \dots + x_{k-1} B^0 \\ up_x &= x_0 B^0 + x_1 B^1 + \dots + x_{k-1} B^{k-1} \end{align*}$$

Where ~x_0, x_1, \dots, x_{k-1}~ is an array of colors on the path from ~R~ to ~X~ (~color(R) = x_0~, ~color(X) = x_{k-1}~) and ~B~ is the value of the hash basis. These two values can be determined using a single DFS traversal of our tree. The path from ~R~ to ~X~ is a palindromic segment if ~down_X = up_X~ holds. If we root the tree in every node and apply this procedure, we will cover all cases. The complexity of this algorithm is ~\mathcal O(N^2)~.

The second subtask is a classic, well-known problem of finding the longest palindromic substring which can be solved using Manacher's algorithm.

The solution for the third subtask is quite similar to the solution of the second subtask. The only difference is that we must apply Manacher's algorithm on a path between every pair of leaves.

We will begin our solution for the whole problem with the following observation: If there exists a palindromic segment of length ~K > 2~, then there exists a palindromic segment of length ~K-2~. Therefore, we can use binary search on even and odd lengths to find the longest palindromic segment.

But, how do we check if a palindromic segment of fixed length exists in a given tree? To answer that question, we will first solve an easier version of that problem – we will check if there is a palindromic segment of a fixed length that contains the root of our tree, node ~R~.

In a rooted tree, a path between two nodes ~A~ and ~B~ consists of two tree branches, where the length of path on one branch is greater or equal to the length on the other branch. We will divide the path between ~A~ and ~B~ into three parts: path from ~A~ to ~C~, path from ~C~ to the root and path from the root to ~C~, where ~C~ is chosen such that the lengths ~A-C~ and ~R-B~ are equal. Note that ~C~ is uniquely defined by the node ~A~, since we only care about palindromes of fixed size. In order to check whether the path from ~A~ to ~B~ is a palindromic segment, it is enough to check the following:

• (1) Path from ~R~ to ~C~ is a palindrome (depicted in red)
• (2) Colors from ~C~ to ~A~ are the same as colors from ~R~ to ~B~ (depicted blue).

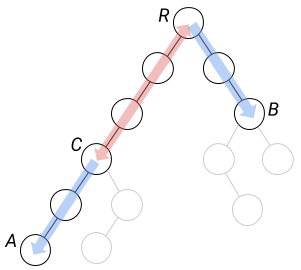
For each node of the tree, we will calculate the values ~down_X~ and ~up_X~ in advance in the same manner as it was described in the solution of the first subtask. The first check is simply done by comparing ~down_C~ and ~up_C~. The second check can be done by comparing the values:

• ~down_B~
• (3) ~down_A - down_{par(C)} \times B^{dep(A)-dep(C)}~, where ~par(C)~ is the parent of node ~C~ and ~dep(X)~ is the depth of node ~X~.

Now we know how to efficiently check whether the path from ~A~ to ~B~ is a palindromic segment, but that is still not enough because there are ~\mathcal O(N^2)~ such pairs ~(A, B)~. Let's try to observe the problem from another angle: If we fix ~A~, is there (at least) one ~B~ that satisfies all the conditions? Let ~S_B~ be a set of hashes in which we will insert values ~down_B~ of all nodes ~B~ of our tree. Then, for a fixed ~A~, we can simply check condition (1) and we can check condition (3) by finding the corresponding value in ~S_B~. We can assume that the complexity of all operations with ~S_B~ is constant if we use a hash table (std::unordered_set in C++, for example). The complexity of the whole check is therefore ~\mathcal O(N)~.

Note: during implementation you need to make sure that the lowest common ancestor of nodes in ~S_B~ and ~A~ is the root node ~R~.

Now that we know whether a palindromic segment of certain length which passes through the root ~R~ exists, we can use centroid decomposition. If we perform this check for every decomposed subtree with the centroid as a root, we will cover all the cases. With centroid decomposition and a binary search, we end up with an algorithm of complexity ~\mathcal O(N \log^2 N)~.