Little Fabian got a one-dimensional jigsaw puzzle that consists of ~N~ pieces. He quickly realized that each piece belongs to one of the following types:

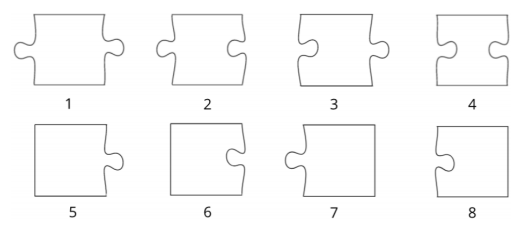
Additionally, it is known that among those ~N~ pieces there is exactly one piece of either type ~5~ or type ~6~ (left border) and exactly one piece of either type ~7~ or type ~8~ (right border).

Fabian wishes to arrange all of the pieces into a single row such that the first (leftmost) piece is of type ~5~ or ~6~ and the last (rightmost) piece is of type ~7~ or ~8~. Two pieces can be placed next to each other if and only if their neighbouring borders are of different shapes, i.e., one has a bump (also called outie or tab) and the other has a hole (also called innie or blank).

Simply solving the puzzle would be too easy for Fabian so he decided to write a unique positive integer on each of the pieces. Now he is interested in finding the lexicographically smallest solution to the jigsaw puzzle. The solution ~A~ is considered lexicographically smaller than solution ~B~ if at the first position (from the left) ~i~ where they differ it holds that the number written on ~i~-th puzzle in ~A~ is smaller than the number written on ~i~-th puzzle in ~B~.

Note: the pieces cannot be rotated.

Input

The first line contains an integer ~N~ ~(2 \le N \le 10^5)~ from the task description.

The next ~N~ lines contain two integers ~X_i~ ~(1 \le X_i \le 8)~ and ~A_i~ ~(1 \le A_i \le 10^9)~ which represent the type of the ~i~-th piece and the number Fabian wrote on it. All numbers ~A_i~ will be different.

Output

If Fabian cannot solve the jigsaw puzzle, you should output -1 in a single line.

Otherwise, you should output the numbers that are written on the pieces in the lexicographically smallest solution to the puzzle.

Scoring

In test cases worth a total of ~5~ points it will hold ~N \le 4~.
In test cases worth additional ~5~ points it will hold ~N \le 10~.
In test cases worth additional ~10~ points pieces of types ~2~ and ~3~ will not appear in the input.
In test cases worth additional ~20~ points there will be at most one piece of type ~1~ or ~4~.

If for some test case in which the solution to the puzzle exists, you output the correctly solved puzzle but your solution is not lexicographically smallest, you will get ~40\%~ of the points intended for that test case.

Sample Input 1

5
1 5
2 7
2 3
8 4
6 1

Sample Output 1

1 3 7 5 4

Explanation For Sample 1

There are only two possible solutions to the puzzle:

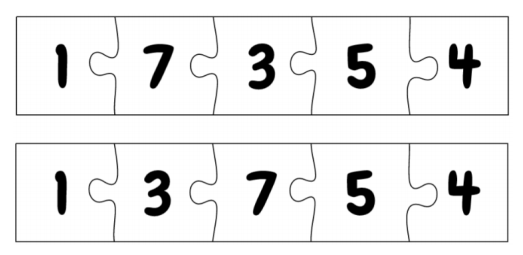
We can see that the second depicted solution has a smaller number written on the second piece. Therefore, that is the lexicographically smallest solution.

Sample Input 2

3
5 1
7 2
4 3

Sample Output 2

1 3 2

Sample Input 3

5
2 5
2 7
2 3
8 4
6 1

Sample Output 3

-1