Since he learnt how to solve the Rubik's cube, Jurica has also been interested in other puzzles of this kind and he recently created an enigmatic toy himself. We can imagine Jurica's puzzle as a triangular net in the form of a parallelogram whose nodes are arranged in $N$ rows and $M$ columns. The rows are labeled from $1$ to $N$ from the bottom up, and the columns are labeled $1$ to $M$ from left to right. Each node is denoted by coordinates $(x,y)$, where $x$ is the row and $y$ is the column. Each node has a unique integer value between $1$ and $N\cdot M$ written in it, and the puzzle is considered solved when the first row contains numbers from $1$ to $M$ ordered from left to right, the second row contains numbers from $M+1$ to $2M$ in the same order, etc. The picture below shows a solved puzzle of 3 rows and 4 columns.

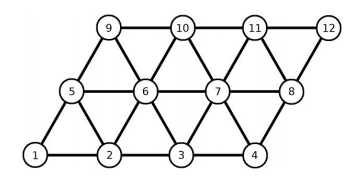
The layout of the puzzle can be changed in two ways:

1. By selecting the unit sized rhombus whose nodes are determined by the coordinates $(x,y)$, $(x+1,y)$, $(x+1,y+1)$ and $(x,y+1)$, and rotating the node values in the clockwise direction.

   

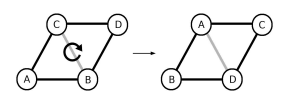
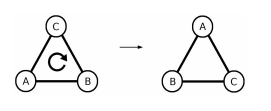
2. By selecting a unit sized equilateral triangle whose nodes are determined by the coordinates $(x,y)$, $(x+1,y)$ and $(x,y+1)$, and rotating the node values in the clockwise direction.

   

On one boring day, Jurica scrambled the puzzle, writing down the moves he had made on a piece of paper. This sequence of moves he called a mega-move, and explained the application of mega-move as the sequential application of the moves written on the paper. After that, he has repeatedly made the same mega-move several times. He noticed an unusual regularity soon. Starting from a solved puzzle, after exactly $K$ mega-moves, the puzzle will again be solved (the first time since applying the mega-moves).

For given integers $N$, $M$ and $K$, determine if there is a mega-move that will allow Jurica to solve the puzzle after exactly $K$ repetition of that mega-move, and if so, print that sequence of moves. Note: The solution is not necessarily unique and does not have to be optimal in the number of moves, but the number of moves is limited (see section Input).

Input Specification

The first line contains three integers $N,M$ $(2\le N,M\le 100)$ and $K$ $(2\le K\le {10}^{12})$, the numbers from the task description.

Output Specification

If there is not such a mega-move that meets the conditions from the task, print -1 in the only line.

Otherwise, print the number of moves $B$ $(1\le B\le 500000)$ in the first line and in the following $B$ lines one move in the following form:

• R x y (without the quotation marks) if it is a rotation of a rhombus (operation 1), or
• T x y (without the quotation marks) if it is a rotation of an equilateral triangle (operation 2), whereas the coordinate $(x,y)$ represents the bottom left node of the rhombus or the triangle and it holds that $1\le x<N$ and $1\le y<M$.

Constraints

In the test samples worth 40% of the points it will hold that $N,M\le 3$ and $K\le 20$.

Sample Input 1

2 3 2

Sample Output 1

5
R 1 1
R 1 1
T 1 1
T 1 1
T 1 1

Sample Input 2

3 3 12

Sample Output 2

3
R 1 1
T 2 2
T 2 1

Sample Input 3

5 4 116

Sample Output 3

-1