Valerija works as a valet at a fancy restaurant. Her job is to wait for the arrival of distinguished guests, politely greet them, obtain the keys of their vehicles, and park their vehicles at a nearby parking lot. Once the event is over, she makes sure that each of the guests regains custody of their vehicle and happily leaves the venue.

One evening, shortly after she finished parking all of the vehicles, she noticed a particularly interesting property regarding their colors. Namely, it turned out there were exactly ~2N~ vehicles at the parking lot, and they were colored in ~N~ different colors, such that there were exactly two vehicles of each color. We denote the colors of the vehicles by integers from ~1~ to ~N~.

The parking lot itself is organized as a sequence of ~M~ parking spaces, denoted by integers from ~1~ to ~M~, where each parking space can contain at most two vehicles. There is only one entrance to a parking space, and a vehicle can enter or exit the space if no other vehicle is blocking the entrance. We'll call the vehicle parked closer to the entrance the top vehicle, and the vehicle parked further from the entrance the bottom vehicle. Valerija parked the vehicles in such a way that each parking space is either empty, full (i.e. contains two vehicles), or contains a single bottom vehicle.

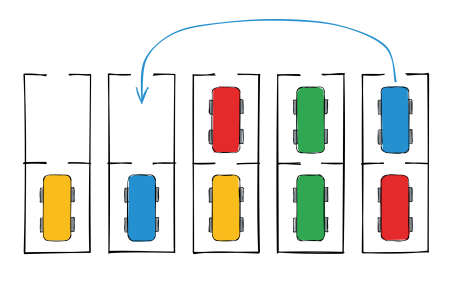
Valerija would like to repark the vehicles so that each pair of vehicles of the same color is parked in the same parking space. She doesn't care which parking space will contain which color, and which specific vehicle will be at the top or bottom of the parking space. She will repark the vehicles in a series of drives. In each drive, she will sit in a parked vehicle that is able to exit its current parking space, and will drive it to another parking space that is either:

• empty, in which case she parks it as a bottom vehicle, or
• contains a single parked vehicle of the same color as the one she's currently driving, in which case she parks it as a top vehicle.

Valerija wants to minimize the number of drives needed to repark the vehicles according to her wishes. Your task is to help her by finding the shortest sequence of drives that would achieve her goal, or determine that no such sequence exists.

Input Specification

The first line contains two space-separated integers ~N~ and ~M~ from the task description.

The ~i~-th of the next ~M~ lines contains two space-separated integers ~b_i~ and ~t_i~ ~(0 \le b_i, t_i \le N)~ that describe the ~i~-th parking space. More precisely, the number ~b_i~ represents the bottom vehicle color, and the number ~t_i~ represents the top vehicle color. If a position in the parking space is empty, the corresponding integer will be equal to ~0~. It is guaranteed that no parking space contains only a top vehicle, i.e. if ~b_i = 0~, then ~t_i = 0~ as well.

Output Specification

If there is no sequence of drives that could repark the vehicles according to Valerija's wishes, print -1 in the only line.

Otherwise, the first line should contain an integer ~K~, the smallest number of drives needed to satisfy Valerija's goal.

The ~i~-th of the next ~K~ lines should describe the ~i~-th drive. More precisely, it should contain two integers, ~x_i~ and ~y_i~ ~(1 \le x_i, y_i \le M, x_i \ne y_i)~, representing that Valerija should take a vehicle from parking space ~x_i~ to parking space ~y_i~ in the ~i~-th drive. Of course, the ~x_i~-th parking space must contain at least one vehicle at that point, and the vehicle closer to the entrance must be movable to parking space ~y_i~, i.e. parking space ~y_i~ must be either empty or contain a vehicle of the same color.

Constraints

For all subtasks:

~1 \le N \le M \le 200\,000~

If your solution correctly determines the smallest number of drives in all test cases of a certain subtask, but incorrectly outputs the description of drives in some of them (or doesn't output it at all), it will receive ~20\%~ of the points allocated to that particular subtask.

Subtask	Score	Constraints
~1~	~10~	~M \le 4~
~2~	~10~	~2N \le M~
~3~	~25~	All parking spaces are initially either empty or full, and ~N \le 1\,000~.
~4~	~15~	All parking spaces are initially either empty or full.
~5~	~25~	~N \le 1\,000~
~6~	~15~	No additional constraints.

Sample Input 1

4 5
1 0
2 0
1 3
4 4
3 2

Sample Output 1

3
5 2
3 5
3 1

Explanation for Sample 1

The image from the task description depicts the initial state of the parking lot in this example. Notice that in this case, each drive is forced, i.e. there is only one valid first drive, only one valid second drive, and two equivalent third drives, after which we reach the end goal.

Sample Input 2

4 5
0 0
2 1
3 1
3 4
2 4

Sample Output 2

-1

Sample Input 3

5 7
1 0
2 1
2 3
4 3
5 4
5 0
0 0

Sample Output 3

6
2 1
3 7
4 7
2 3
5 4
5 6