Prepared by: Ante Ðerek, Luka Kalinovčić, Paula Vidas, and Dominik Fistrić

Fun fact: This task was originally prepared for CEOI 2013 (also in Croatia). However, it was deemed too difficult, especially because the contestants didn't have full feedback back then, and thus it didn't appear on the contest. Task idea was proposed by Ante Ðerek and solution was found by Luka Kalinovčić. To honor them, this year's statement featured Ante and Luka as the main characters.

Note that in any tree with maximum degree at most three, we can always find a node with degree at most two. If we root the tree in such a node, every node will have at most two children (i.e. it's a binary tree).

Let's start with the first subtask. Let ~P_1, \dots, P_N~ be the given points, such that they form vertices of a convex polygon in that order. Place the root of the binary tree in any of the points, say ~P_1~. Let ~k~ be the size of the subtree of one of its children. We can place this child in node ~P_2~ and decide to place its whole subtree in points ~P_2, \dots, P_{k+1}~ in some way. If the node has two children, we place the second child in node ~P_{k+2}~ and its subtree in ~P_{k+2}, \dots, P_N~. We then solve the subproblems recursively. A careful implementation of this strategy has complexity ~\mathcal O(N \log N)~.

We will now describe a solution for subtasks 2 and 3. Similarly to subtask 1, place the root in some point ~A~ on the convex hull of the given point set. Sort all other points by the polar angle around point ~A~. In other words, we will sort them such that if point ~B~ is before point ~C~, then points ~A, B, C~ are ordered counter-clockwise. Again, if ~k~ is the subtree size of a child, place this child's subtree in the first ~k~ points, choosing the first of the points as the one where the child goes. If there are two children, the other child's subtree is placed in the remaining points, and the child is placed in the first of them.

Time complexity of this approach is ~\mathcal O(N^2 \log N)~ if we sort the points each time, which is enough for the second subtask. It can be sped up to ~\mathcal O(N^2)~ if we use some selection algorithm with expected complexity ~\mathcal O(N)~ (e.g. std::nth_element in C++) to find the ~k^\text{th}~ smallest element. This is fast enough to pass the third subtask.

Finally, we describe the full solution. Notice that for now, we used a procedure that takes a set of points with one distinguished point on the hull, and a tree with one distinguished node, and draws the tree on those points, such that the distinguished node is placed in the distinguished point. It turns out that it's possible to design a procedure that does the same but given two pairs of distinguished points and nodes, such that the points lie on the hull and are adjacent.

The high-level idea is the following: If we're given one point-node pair ~(A, a)~, such that ~A~ is on the hull and the tree is rooted in ~a~, then we choose some leaf ~b~ and one of the adjacent points on the hull as ~B~, and ~(B, b)~ is our second pair, so we're in the two pair case. Assume now we're given two point-node pairs ~(A, a)~ and ~(B, b)~, such that ~a~ is the root of the tree, while ~b~ is a leaf, and ~A~ and ~B~ are two adjacent points on the hull. Take ~c~ to be some node on the path between ~a~ and ~b~, and take ~C~ to be a point such that the gray triangle ~ABC~ doesn't contain any other points.

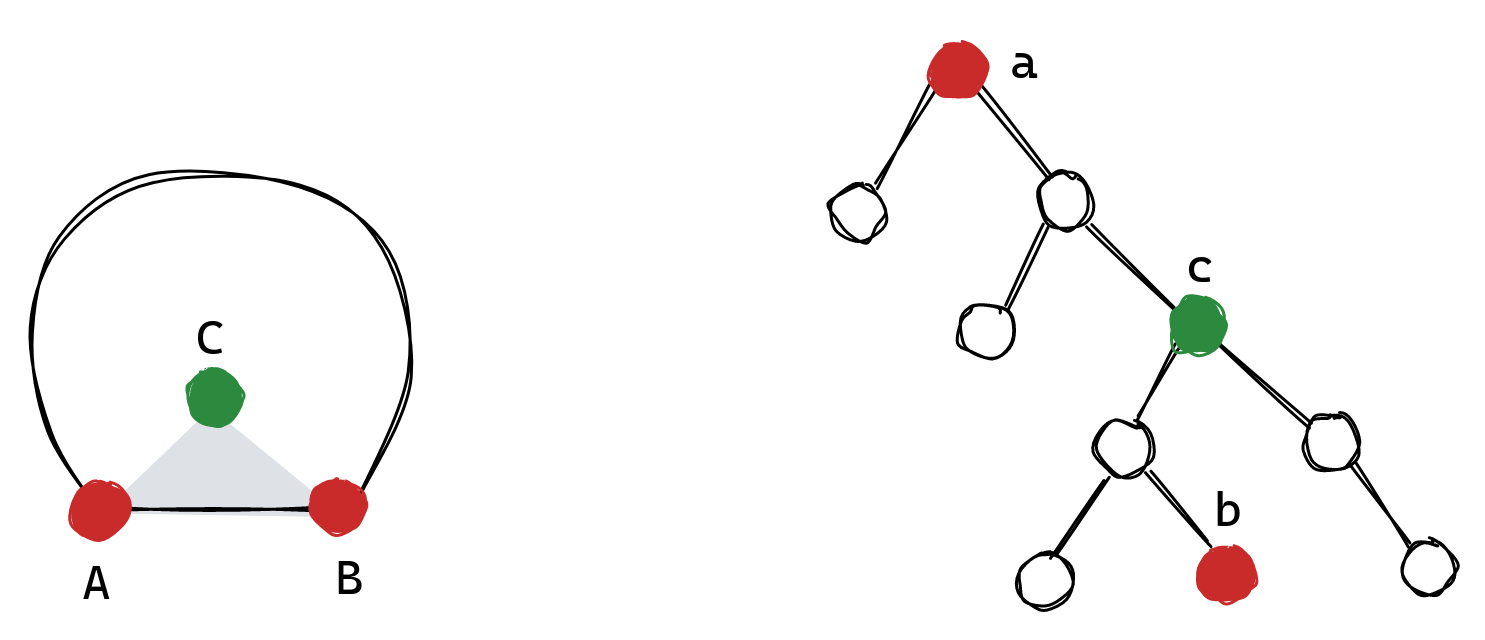
Then, we can construct three subproblems, blue, green, and yellow, shown in the figure below. The blue, green, and yellow regions are chosen such that the number of points in each region matches the size of the respective tree, and the points in a region form a consecutive subsequence if we sort all points by polar angle around ~C~. We distinguish two cases, when ~C~ is not on the hull and when it is.

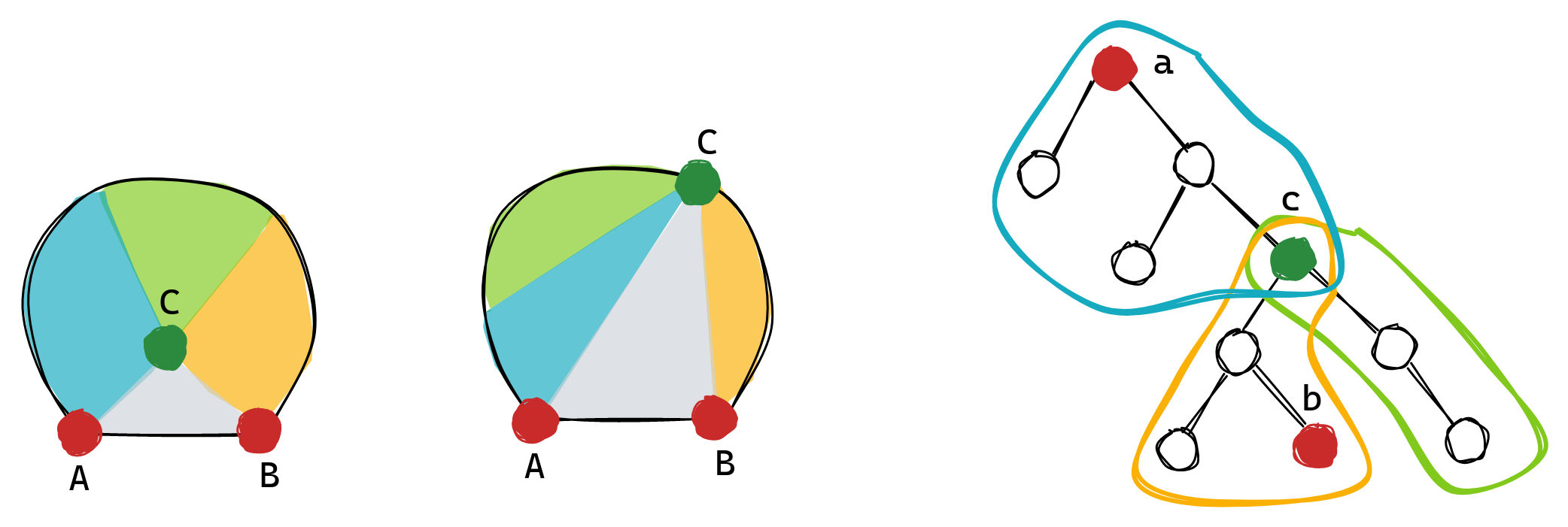
It can be proven that there always exists a "good" point ~C~, i.e. a point such that the gray region has no other points inside, ~AC~ is a line segment on the hull of the blue region, ~C~ is on the hull of the green region, and ~BC~ is a line segment on the hull of the yellow region. This is left as an exercise for the reader.

The three subproblems can be solved recursively. In the blue problem we're given point-node pair ~(A, a)~ as root and ~(C, c)~ as leaf, in the yellow problem we're given point-node pair ~(C, c)~ as root and ~(B, b)~ as leaf, and in the green problem we're given a point-node pair ~(C, c)~ as root.

Now it's time to analyse the time complexity.

When choosing nodes ~b~ or ~c~, it's not optimal to simply take any node. When we're given root ~a~ and need to choose a leaf ~b~, we'll do it this way: start from the root, and at each step move down to the "heavy" child, i.e. the one with the larger subtree size, until a leaf is reached. When we're given root ~a~ and leaf ~b~, for node ~c~ we'll take the midpoint of the path between ~a~ and ~b~.

Consider a two point-node pair subproblem with ~N~ nodes. Let ~k~ denote the length of the path from ~a~ to ~b~, and let's look at the subtrees attached to this path that belong to the "light" children. Denote the sizes of these subtrees as ~N_1, N_2, \dots, N_k~. Notice that ~N_1+N_2+\dots+N_k \le N~, and ~N_i \le \frac N 2~ for all ~i = 1, 2, \dots, k~, because they are the light children. Note that each subproblem can be solved in time that is linear in the size of the subproblem (not counting the recursive calls). Therefore, after ~\log N~ steps of the process described above, we'll reach all the subproblems of size ~N_i~, and will have spent ~\mathcal O(N \log N)~ time up that point. Consequently, if ~T(N)~ denotes the time required to solve a subproblem of size ~N~, we obtain:

$$\displaystyle T(N) = \sum_{i=1}^k T(N_i) + \mathcal O(N \log N)$$

This recurrence relation works out to be ~T(N) = \mathcal O(N \log^2 N)~.

If in each subproblem we sort the points by angle, a factor of ~\log N~ is added to the complexity, and that solution is fast enough for subtask 4. However, sorting is not necessary if we use std::nth_element, and that solution should achieve full score for this task.