Subtask 1 was intended to permit simple case-analysis based solutions.

Subtask 2 was intended to permit brute force search solutions.

Subtask 3 was a reduction to a standard Dynamic Programming problem (commonly stated as: you have certain coins, find if you can pay exactly ~X~ amount of money with them).

Subtask 4 was intended to permit task-specific but suboptimal Dynamic Programming solutions.

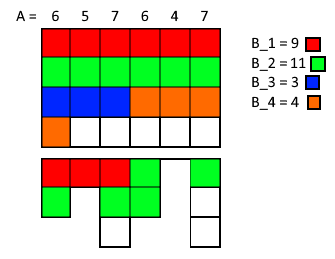
The full solution uses Dynamic Programming. Let us mentally reorder the hours spent on each meal such that for the first ~K~ hours, all chefs are different. This way we can visualize these ~K~ hours forming an ~N \times K~ "diversity box", with all "non-diverse hours" coming afterwards (as shown in the figure above). Now let's make the following observations:

1. Each chef can add at most ~1~ hour to any column of the "diversity box".
2. A chef ~j~ can fill the "diversity box" by at most ~\min(B_j, N)~.
3. In a correct solution, the "diversity box" must be filled by an amount of at least ~N \times K~.
4. Suppose you have decided to hire chefs for a total of ~H~ hours. Then it's optimal to hire such set of chefs that the "diversity box" is filled as much as possible (perhaps even overfilled).

Now let ~D[c][h]~ be the maximum amount we can fill the "diversity box" by picking a subset of chefs ~1, \dots, c~ such that they are hired for a total of ~h~ hours. Now let us notice that for the value ~D[c][h]~ there are two possibilities:

1. The maximal subset contains chef ~c~. Thus the other chefs in this subset form a maximal solution for ~D[c-1][h-B_c]~ (otherwise we could pick a better subset). Thus ~D[c][h] = D[c-1][h-B_c] + \min(B_c, N)~.
2. The maximal subset doesn't contain chef ~c~. Thus this subset also forms a maximal solution for ~D[c-1][h]~ (a better solution to ~D[c-1][h]~ would contradict the maximality of this subset). Thus ~D[c][h] = D[c-1][h]~.

Now we simply need to consider the two cases and see which gives us a better solution. Thus ~D[c][h] = \max(D[c-1][h-B_c] + \min(B_c, N), D[c-1][h])~. For performing the dynamic programming computation, we can initialize ~D[0][0]~ to ~0~ and every other ~D[i][j]~ to ~\infty~. Note that once we have computed ~D[c][*]~ we don't care about ~D[c-1][*]~ anymore, so we can optimize memory consumption. The answer will be minimum non-negative ~h - \sum_i A_i~ such that ~D[N][h] \ge N \times K~.

Credits

• Task: Bernhard Linn Hilmarsson (Iceland)
• Solutions and tests: Oliver-Matis Lill, Andres Unt (Estonia)