Baltic Olympiad in Informatics: 2016 Day 1, Problem 3

A grid of size ~(2n+1) \times (2n+1)~ has been constructed as follows. Number ~1~ has been placed in the center square, number ~2~ has been placed to the right of it, and the following numbers have been placed along the spiral counterclockwise.

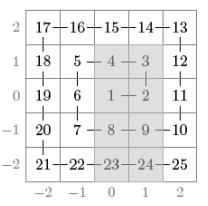
Your task is to calculate answers for ~q~ queries where the sum of numbers in a rectangular region in the grid is requested (modulo ~10^9+7~). For example, in the following grid ~n=2~ and the sum of numbers in the gray region is ~74~:

Constraints

For all subtasks:

~1 \le q \le 100~

Subtask 1 [12%]

~1 \le n \le 1\,000~

Subtask 2 [15%]

~1 \le n \le 10^9~

~x_1 = x_2~ and ~y_1 = y_2~

Subtask 3 [17%]

~1 \le n \le 10^5~

Subtask 4 [31%]

~1 \le n \le 10^9~

~x_1 = y_1 = 1~

Subtask 5 [25%]

~1 \le n \le 10^9~

Input Specification

The first input line contains two integers ~n~ and ~q~: the size of the grid and the number of queries.

After this, there are ~q~ lines, each containing four integers ~x_1~, ~y_1~, ~x_2~ and ~y_2~ ~(-n \le x_1 \le x_2 \le n, -n \le y_1 \le y_2 \le n)~. This means that you should calculate the sum of numbers in a rectangular region with corners ~(x_1, y_1)~ and ~(x_2, y_2)~.

Output Specification

You should output the answer for each query (modulo ~10^9+7~).

Sample Input

2 3
0 -2 1 1
-1 0 1 0
1 2 1 2

Sample Output

74
9
14