Editorial for Baltic OI '13 P3 - Pipes
Submitting an official solution before solving the problem yourself is a bannable offence.
Task
A connected, simple, graph on vertices and
edges is given. Weights are assigned to
all edges (they are integers but need not be positive). These weights are not known but
for each vertex the sum of weights of the edges incident to it is given. Can the weights be determined uniquely? If yes, what are they?
Intended Solution
We will use graph theoretic terminology, seeing reservoirs as vertices and pipes as edges of a graph . For each edge
, let
be its weight. We allow
to take integer values, with the following interpretation:
- if
then
of water is pumped into
,
- if
then
of water is drained from
.
For each vertex , we know
which is the sum of weights of the edges incident to (
is the set of such edges). Note
that
gives
linear equations for
unknowns
. There can be a unique solution only if
(this is true even for integer values of
)
. Moreover, as
is connected,
.
Suppose . Then
is a tree and has a leaf (a vertex of degree one, that is,
with exactly one incident edge). Pick a leaf
and let
be the vertex to which
is joined by an edge. Then
gives
which is known. Remove
together with the edge
from
and subtract
from
. The remaining graph is again a tree. Continue this process until a single vertex remains. Then
has a unique solution which we have found.
Now suppose . Remove leaves as before, until there are no more leaves. What
remains is a connected graph on
vertices and
edges where
is the number of leaves removed. This is a cycle of length
. If
is even then there are multiple solutions (see Fig. 1).
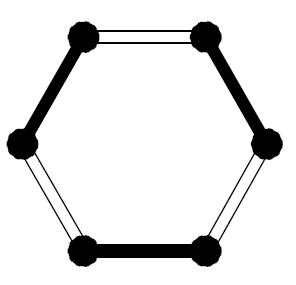
If is odd, however, we have a unique solution. Indeed, suppose
are the vertices in this order. From
we have
so
This determines uniquely and having its value we can easily fill in the remaining weights:
,
and so on.
If , we know from earlier considerations that there is more than one possible
solution.
Given a connected graph on
vertices, we can do this in total time
: find the initial leaves of
and put them in a stack. Consider the top leaf: remove it and decrease the degree of its neighbour. Check if this degree is one: if yes, add the neighbour to the stack. Do this until no leaves remain. So the total time complexity is
.
Remark
Observation can be made purely by combinatorial considerations without using any
linear algebra. If
is connected on
vertices and at least
edges then it contains at least two cycles. If one of them has even length, there cannot be a unique solution (Fig. 1). Assume they both have odd length. There are two cases.
- The cycles have at most one vertex in common. As
is connected, there is a path
that joins the cycles (we allow
to be a single vertex). In Fig. 2, on the left is the case when
has even length (that is,
has an even number of edges) and on the right is the case when
has odd length. In both cases, there is more than one solution.

- The cycles share at least two vertices. Let
be one of the common vertices. Start at
and follow one of the cycles until it intersects the other cycle. Let this intersection point be
. There are three paths joining
and
, any pair of which intersect only at endpoints (see Fig. 3. Let
,
and
be their lengths. Pairs of these paths form cycles of lengths
,
and
. At least one of these numbers is even so there is a path of even length. Referring back to Fig. 1, we know there cannot be a unique solution.
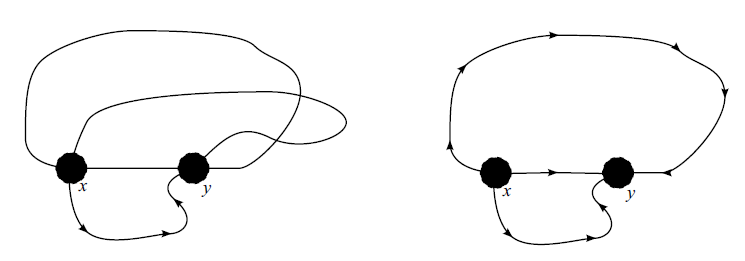
Comments