Editorial for Baltic OI '07 P1 - Escape
Submitting an official solution before solving the problem yourself is a bannable offence.
The soldiers and the canyon can be modeled as an undirected graph : Let each soldier be represented by one vertex, where there is an edge between two vertices if and only if areas visible by the two corresponding soldiers intersect or touch, i.e. the distance between the two soldiers is less than or equal to
. Let there be two additional vertices
and
, where
represents the northern side of the canyon and
the southern side of the canyon. Let these vertices be connected to all vertices representing soldiers who can see the respective side of the canyon, i.e. whose distance from the side is at most
meters.
Now it is fairly easy to decide if the canyon can be passed safely. Just perform either depth-first-search or breadth-first-search to check whether there is a path between and
in
. If that is the case, then there exists a continuous chain of areas visible by some soldier that connects the northern and southern sides of the canyon, thus keeping the prisoners from passing it. Vice versa, if there is no such chain of visible areas, the canyon can clearly be passed safely.
Deciding how many soldiers must be eliminated in order to pass the canyon safely is a bit more complicated. Since the canyon can be passed safely if and only if there is a path between and
in
, one has to find
-vertex-connectivity of
, i.e. how many vertices in
have to be deleted in order to disconnect
and
. This is essentially a minimum cut problem. It can be solved by setting edge capacities to
, vertex capacities to
and finding the maximum flow from
to
(contrary to the standard minimum cut problem for edges, where vertex capacities are set to
and edge capacities to
). To make a standard maximum flow algorithm applicable, vertex capacities have to be eliminated, though. This can be done relatively easily by constructing a directed graph
, where each vertex of
except
and
is replaced by two vertices, in-vertex and out-vertex. If edges in
are set according to figure 2.1 below, then the maximum flow from
to
in
will be equal to the maximum flow from
to
in
. Since there are no vertex capacities in
, this maximum flow and hence
-vertex-connectivity of
can now be found using standard maximum flow algorithm.
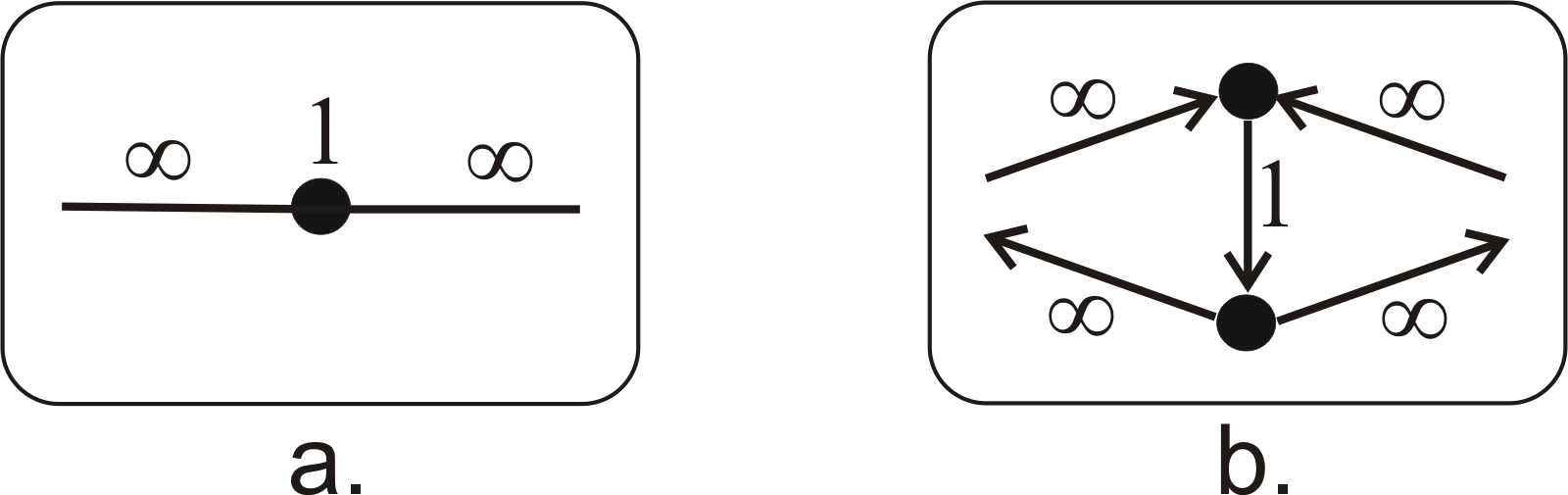
Figure 2.1: Converting a vertex capacity (a) to an edge capacity (b)
Comments