Consider the following maze made of equilateral triangles:

Each vertex is described by two coordinates $x$ and $y$ as in the picture. Some of the edges have a white or a black circle on them. There are two major rules that control movement within the maze:

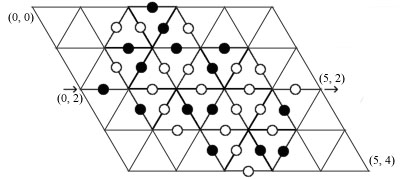
• it is only allowed to pass edges with circles on them.
• while walking through the maze it is obligatory to alternate white and black circles; i.e. it is only allowed to pass an edge with white circle if the last circle passed was black and vice versa. It is allowed to pass an edge with either black or white circle on it during the first move.

Task

Write a program to find the length of the shortest path from the entrance point to the exit in the maze. The length of the path is defined as the number of edges (or circles) passed. You may assume that such path always exists.

Input Specification

The first line contains two integers $W$ and $H$ which are the width and the height of the maze respectively ($1\le W,H\le 500$). The second line consists of four integer values: $X_1,Y_1,X_2,Y_2$ ($0\le X_1,X_2\le W;0\le Y_1,Y_2\le H$). $(X_1,Y_1)$ are the coordinates of the entry point in the maze and $(X_2,Y_2)$ are the exit coordinates.

The next $2H+1$ lines provide the description of the edges: odd lines (3^rd, 5^th, etc) describe horizontal edges, and even lines (4^th, 6^th, etc) describe non-horizontal ones. Each line consists of a string of characters n, w and b, where n means, that there is no circle on the edge, and w or b means that there is white or black circle on the edge respectively. There are no spaces between these characters. Naturally, odd lines consist of exactly $W$ characters, and even lines consist of exactly $2W+1$ characters.

Output Specification

Your program should output a single integer (the length of the shortest path from entrance point to the exit in the maze) in the first (and the only) line of the output.

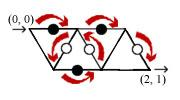
Sample Input 1

2 1
0 0 2 1
bb
nwwnw
bn

Sample Output 1

6

Explanation for Sample Output 1

A simple maze. One possible shortest path is this: $(0,0)\to (1,0)\to (0,1)\to (1,1)\to (1,0)\to (2,0)\to (2,1)$

Here is the illustration of the maze and the shortest path:

Sample Input 2

5 4
0 2 5 2
nnbnn
nnnwwbwnnnn
nbbbn
nnwbwwbwwnn
bwwww
nnbwbbwwbnn
nwwwn
nnnnbwbbnnn
nnwnn

Sample Output 2

22

Explanation for Sample Output 2

This is the description of the maze given in the picture on the first page. The shortest path is this:

$${\displaystyle \begin{array}{l}(0,2)\to (1,2)\to (1,1)\to (2,1)\to (2,0)\to \\ (3,0)\to (3,1)\to (3,2)\to (4,1)\to (3,1)\to \\ (3,0)\to (2,0)\to (2,1)\to (1,1)\to (1,2)\to \\ (1,3)\to (2,3)\to (2,4)\to (3,4)\to (3,3)\to \\ (4,3)\to (4,2)\to (5,2)\end{array}}$$

(Length: 22)