Baltic Olympiad in Informatics: 2004 Day 2, Problem 3

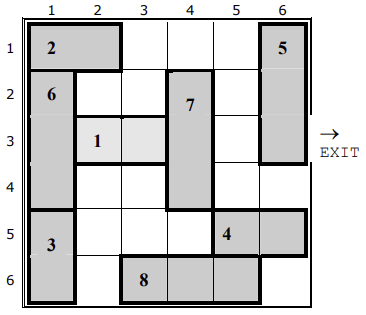
The youth hostel at which the Baltic Olympiad in Informatics 2004 is being held has a parking lot consisting of a $6\times 6$ grid. Lot's rows are numbered starting from $1$ to $6$ consecutively from top to down, columns are numbered in the same way from left to right. There is only one exit from the lot at the right side of third row.

On that lot, there are $N$ parked cars. Your car is among those cars, but unfortunately, there is no easy way out because your car is blocked by the other cars. You and your friends can move the cars forwards and backwards however, since the gearbox of all cars is in Neutral. You may not steer or turn, neither your own car nor any of the other cars.

It is your task to determine the minimum number of steps necessary to get your car of size $2\times 1$ squares off the parking lot. One step means moving one car one square. None of the other cars may be moved off the parking lot.

There are only two types of cars. One type is $2\times 1$ squares in size, whereas the other type occupies $3\times 1$ squares. Cars may only be moved along the longer one of their two axes.

Constraints

$1\le N\le 16$

$1\le x_i,y_i\le 6$

$l_i\in \{2,3\},o_i\in \{0,1\}$

Input Specification

The first line of the input contains the number of cars $N$.

Each of the subsequent $N$ lines contains the description of the car that is labeled with the number $i$. Each line consists of four space-separated integers specifying the length $l_i$, the orientation $o_i$, and the start (upperleft) coordinates $x_i$ (number of column) and $y_i$ (number of row). $o_i=1$ means that the car is parked horizontally. Otherwise, it is parked vertically.

Your car is described in the first line following the single line consisting of the number $N$ (i.e. the second line of the input). Your car has to exit the parking lot using the only possible exit.

Output Specification

Output a single integer, representing the minimum number of steps necessary to exit the parking lot in your car.

If it is impossible to exit the parking lot, print $-1$.

Sample Input

8
2 1 2 3
2 1 1 1
2 0 1 5
2 1 5 5
3 0 6 1
3 0 1 2
3 0 4 2
3 1 3 6

Sample Output

18

Sample Explanation

The sample corresponds to the diagram in the problem statement.

In the given example $N=8$ and your car is labeled with the number $1$. Below is the minimum sequence of length $18$ to exit the parking lot with your car:

$${\displaystyle 4\leftarrow \leftarrow \leftarrow ,2\to ,6\uparrow ,3\uparrow ,8\leftarrow \leftarrow ,5\downarrow \downarrow \downarrow ,7\downarrow \downarrow ,1\to \to \to \to \to }$$