Baltic OI '04 P5 - Rectangles
View as PDFBaltic Olympiad in Informatics: 2004 Day 2, Problem 2
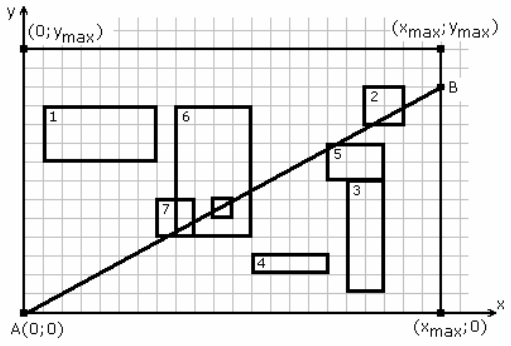
There are given rectangles on the plane. Rectangle sides are parallel to coordinate axis. These rectangles may overlap, coincide or be drawn inside one another. Their vertices have non-negative integer coordinates and
coordinates do not exceed
and
coordinates do not exceed
.
A segment is started in the point and ended in point
. The coordinates of the point
(the other end of the segment) satisfy the following conditions:
- The coordinates of
are integer numbers;
- The point
belongs either to the segment
or to the segment
.
The segment might cross rectangles (we assume that crossing takes place even if only one rectangle vertex is crossed).
Write a program to find a point for which the segment
crosses as many rectangles as possible.
Constraints
Input Specification
The first line of the input contains three space-separated integers: and
.
Each of the following lines contains four space-separated integers: the coordinates of the bottom left corner
and
, and coordinates of the top right corner
and
.
Output Specification
Output three space-separated integers on the first and only line of output.
First output the maximum number of crossed rectangles, followed by the and
coordinates of point
.
If there are several solutions, output any one of them.
Sample Input
22 14 8
1 8 7 11
18 10 20 12
17 1 19 7
12 2 16 3
16 7 19 9
8 4 12 11
7 4 9 6
10 5 11 6Sample Output
5 22 12Sample Explanation
The sample corresponds to the diagram in the problem statement. Another possible solution is 5 22 11.
Comments