Baltic OI '04 P1 - Ships
View as PDFBaltic Olympiad in Informatics: 2004 Day 1, Problem 1
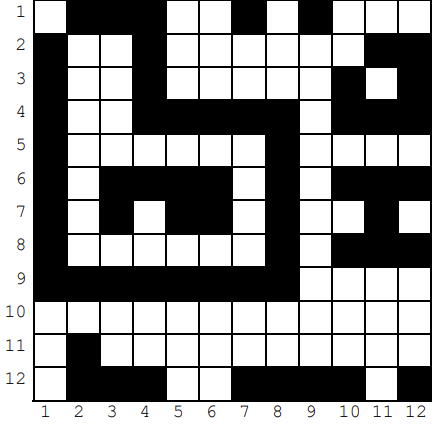
The board of "Ships" game consists of squares. Each square may belong to some ship or be empty. If two squares belong to ships and have a common edge, then both squares belong to the same ship. Squares of different ships have no common points. The tonnage of a ship is the number of squares belonging to this ship.
In the given example, squares belonging to ships are marked black. On the game board there are: one -ton ship, three
-ton ships, two
-ton ships and three one-ton ships.
Write a program which for given description of a game board calculates number of ships and tonnage of each ship.
Constraints
The total number of ships does not exceed .
The tonnage of any ship does not exceed tons.
Input Specification
The first line of input contains one positive integer .
On each of the next lines, there is given information about one board row, consecutively describing groups of squares from left to right, which belongs to ships in one of two formats:
<number_of_square_column>, if square in given column belongs to ship, but squares to the left and to the right are free;<number_of_first_square_column>-<number_of_last_square_column>, if all consecutive squares from first to last (including) belong to ship and squares to the left and to the right from this group are free.
Square groups are separated by commas, each line ends with a semicolon. There are no spaces in lines. If in some board row there are no ship's squares, then the corresponding line contains only one semicolon.
Output Specification
Your program must output information about ships. On each line, there must be exactly two space-separated integers. The first number must be tonnage and second must be number of ships having this tonnage.
Tonnages must be given in decreasing order and tonnage must be outputted only if there is at least one ship having this tonnage.
Sample Input
12
2-4,7,9;
1,4,11-12;
1,4,10,12;
1,4-8,10-12;
1,8;
1,3-6,8,10-12;
1,3,5-6,8,11;
1,8,10-12;
1-8;
;
2;
2-4,7-10,12;Sample Output
29 1
7 3
4 2
1 3Sample Explanation
This sample corresponds to the figure in the problem statement.
Comments
This should probably be an implementation vs graph theory problem type.
maybe both...