There is a rumor that the Scientific Committee is using a special device for encrypting their communication. If you can crack the encryption you could listen to the problems they have prepared and score many points. Last night you got lucky: one of the members forgot their device in a bar. You opened it and looked at the general design:

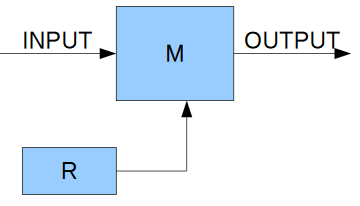
All the operations use 8 bits. XOR is the bitwise exclusive or function (the ^ operator in C, xor operator in Pascal).

$\mathrm{R}$ is a sequence of pseudorandom numbers defined as follows:

• $\mathrm{R}[0]$, $\mathrm{R}[1]$ and $\mathrm{R}[2]$ have secret values only known by the Scientific Committee.
• For $n=3,4,\dots$ let $\mathrm{R}[n]=\mathrm{R}[n-2]\mathrm{XOR}\mathrm{R}[n-3]$.

Furthermore, we have a function $\mathrm{M}$, $\mathrm{M}:[0\dots 255]\to [0\dots 255]$. In fact, $\mathrm{M}$ is a bijection, i.e. when $x\ne y$ it must also be that $\mathrm{M}[x]\ne \mathrm{M}[y]$.

The device used by the Scientific Committee takes one number at a time, and outputs it encrypted. After using the device $N$ times, the next number, $\mathrm{INPUT}$ is encoded as follows:

• $\mathrm{OUTPUT}=\mathrm{M}(\mathrm{INPUT}\mathrm{XOR}\mathrm{R}[N])$

Even though you understand how the encryption device works, you do not know the secret values $\mathrm{R}[0]$, $\mathrm{R}[1]$, and $\mathrm{R}[2]$. Also, you do not know $\mathrm{M}$, so you cannot decode the communication. What you can do instead is play with the device you found. You can give it input numbers and observe the outputs.

Task

Your task is to find out all the secret values: $\mathrm{R}[0],\mathrm{R}[1],\mathrm{R}[2],\mathrm{M}[0],\mathrm{M}[1],\dots ,\mathrm{M}[255]$ with less than $320$ queries (input numbers).

Constraints

• A correct solution receives points only if the number of queries is less than $320$.
• In all tests the secret keys $\mathrm{R}[0],\mathrm{R}[1],\mathrm{R}[2],\mathrm{M}[0],\mathrm{M}[1],\dots ,\mathrm{M}[255]$ are random.
• $0\le \mathrm{INPUT},\mathrm{OUTPUT},\mathrm{R},\mathrm{M}\le 255$

Interaction

This is an interactive program. To play with the encryption module simply write a number between $0$ and $255$ to the standard output. You can then read from the standard input the output of the encryption device, also an integer between $0$ and $255$. When you know the secret values output one line containing the string SOLUTION and after that output $259$ lines: $\mathrm{R}[0],\mathrm{R}[1],\mathrm{R}[2],\mathrm{M}[0],\mathrm{M}[1],\dots ,\mathrm{M}[255]$, one value per line.

Example

Let's assume that $\mathrm{R}[0]=0$, $\mathrm{R}[1]=1$, $\mathrm{R}[2]=3$ and that $\mathrm{M}[i]=(i+1)mod256$.
From here we deduce $\mathrm{R}[3]=1$.